Hi guys,
It'll be much appreciated if anyone could me with any of the below question. Thanks to all!!
Note: please prove all the below using vectors.
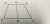
1. In any trapezium ABCD, show the length of MN (which connects the midpoints of the parallel sides of AB and CD) must be half the sum of AC and BD.
2. AB and CD are diameters of a circle with centre O. Prove that ABCD is a rectangle.
3. Prove that the lines joining the midpoints of opposite sides of a quadrilateral ABCD bisect each other.
4. Prove that the medians of a triangle meet at a point that divides each median in the ratio 2:1.
It'll be much appreciated if anyone could me with any of the below question. Thanks to all!!
Note: please prove all the below using vectors.
1. In any trapezium ABCD, show the length of MN (which connects the midpoints of the parallel sides of AB and CD) must be half the sum of AC and BD.
2. AB and CD are diameters of a circle with centre O. Prove that ABCD is a rectangle.
3. Prove that the lines joining the midpoints of opposite sides of a quadrilateral ABCD bisect each other.
4. Prove that the medians of a triangle meet at a point that divides each median in the ratio 2:1.
Last edited: