This is probably actually 2U, but since I thought of this while doing a 4u question, I placed it here 
(feel free to move it if required)
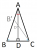
Suppose for any triangle, you find a point such that x = y (refer to below diagram)
would alpha = gamma? (i.e. would a line drawn from it it bisect angle A)
And what about the converse? (i.e. the bisector of an angle bisects the line). That is, if alpha = gamma would x = y?
If it's true, is there a proof for this?
(and if not, why not? if applicable)

(feel free to move it if required)
Suppose for any triangle, you find a point such that x = y (refer to below diagram)
would alpha = gamma? (i.e. would a line drawn from it it bisect angle A)
And what about the converse? (i.e. the bisector of an angle bisects the line). That is, if alpha = gamma would x = y?
If it's true, is there a proof for this?
(and if not, why not? if applicable)