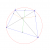
Using geometry theorems, and not coordinate geometry, prove the following:
Suppose the diagonals of the cyclic quadrilateral ABCD intersect at a point G. Draw perpendiculars from G to sides BC and DA, and call these points of intersection as X and Y respectively. Prove that X and Y are symmetric around the line joining the midpoints of AB and CD
Suppose the diagonals of the cyclic quadrilateral ABCD intersect at a point G. Draw perpendiculars from G to sides BC and DA, and call these points of intersection as X and Y respectively. Prove that X and Y are symmetric around the line joining the midpoints of AB and CD