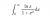
Can someone please help with the question above, but replace ln( x ) with ln^2 (x).
I am asked to prove it equals pi cubed on 8, but when I calculate residue, this is what I get up (maybe with negative) until i apply contour integration, to which the integral converges to 0.
Also, you must use cauchy residue theorem, cant be real analysis.
I dont know why I keep getting 0, I am following methods correctly and using formulae correctly...
