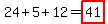dem()sthenes
Member
- Joined
- Jul 18, 2020
- Messages
- 27
- Gender
- Male
- HSC
- 2023
I agree.No lol, that question isn't hard, it's just badly written.
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
I agree.No lol, that question isn't hard, it's just badly written.
Oh yeah. But it applies for every other column. And the shape can't "not be allowed" tbh.One of each shape works, but you could argue that the red heart is not an allowed shape in the first place. Your mirrored statement is just wrong. Take the middle column for instance.
C
lmaoo meAnyone else who just doesn't know wtf is going on and just worrying about trials and whatnot
You can find it in their website. It's either pay or pirate.Where can I find example HAST questions and/or past papers?
Wait I found that online lmao: https://www.algebra.com/algebra/homework/word/numbers/Numbers_Word_Problems.faq.question.978706.htmlFor a number to be divisible by 3 (multiple of 3), its digits must add to a multiple of 3.
I countsets of 3 digits with all digits are odd, and they add to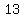
a multiple of 3 (3, 6, 9, 12, 15, 18, 21, 24, or 27).
Those sets are:
{1,1,1} , {1,1,7} ,
{1,3,5} , {1,5,9} ,
{1,7,7} ,
{3,3,3} , {3,3,9} ,
{3,5,7} ,
{3,9,9} ,
{5,5,5} ,
{5,7,9} ,
{7,7,7} , and
{9,9,9} .
Among thosesets,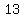 sets have 3 different digits,
sets have 3 different digits,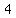
Each of thosesets can be arranged in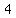 different arrangements/permutations,
different arrangements/permutations,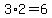
makingdifferent three-digit numbers whose digits are all odd.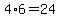
Among thosesets listed above,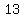
there are alsosets made of just one single repeated digit,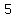
and each one of those sets can be arranged just one way,
to form just one three-digit number,
so from them we can get anotherthree-digit numbers whose digits are all odd.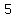
The remainingof the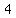 sets listed above contain only two different digits, one of them repeated.
sets listed above contain only two different digits, one of them repeated.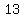
Form each of thosesets, we can make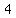 different three-digit numbers,
different three-digit numbers,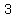
because there are 3 positions to place the unrepeated digit,
and that gives us anotherthree-digit numbers whose digits are all odd.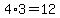
That makes a total ofthree-digit numbers divisible by 3, whose digits are all odd.