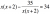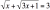-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Help? Algebra (1 Viewer)
- Thread starter zannasheayarrow
- Start date
bleakarcher
Active Member
- Joined
- Jul 8, 2011
- Messages
- 1,503
- Gender
- Male
- HSC
- 2013
x(x+2)-[35/x(x+2)]=34
Let u=x(x+2).
Now, u-[35/u]=34
i.e. u^2-34u-35=0
(u-35)(u+1)=0
Hence, u=-1,35
=>x(x+2)=-1, 35
x^2+2x+1=0 or x^2+2x-35=0
(x+1)^2=0 or (x+7)(x-5)=0
:.x=-1,5,-7
Let u=x(x+2).
Now, u-[35/u]=34
i.e. u^2-34u-35=0
(u-35)(u+1)=0
Hence, u=-1,35
=>x(x+2)=-1, 35
x^2+2x+1=0 or x^2+2x-35=0
(x+1)^2=0 or (x+7)(x-5)=0
:.x=-1,5,-7
nightweaver066
Well-Known Member
- Joined
- Jul 7, 2010
- Messages
- 1,585
- Gender
- Male
- HSC
- 2012
Last edited:
jet
Banned
- Joined
- Jan 4, 2007
- Messages
- 3,148
- Gender
- Male
- HSC
- 2009
You need to be incredibly careful with the second question. If you think about the shape of the graph of

it's half a parabola flipped onto its side. It intersects with y = 3 once so there is only one solution when solving the equation.
However, when you square the second equation, you introduce a second solution. Why? The easiest way for me to show this is with an example. Take for example,
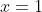
obviously this has one solution, namely, 1. Now, if you instead decided to go through a convoluted method of solving it, you could square it to get

There's a difference here. Both 1 and -1 now solve this equation, all because you squared it. It's essentially because you lost any information about the sign of each side of the equation when you squared it. You could just as easily square
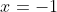
and get the same result.
In the second question above, you will get two solutions. One of the solutions will satisfy the original equation, whilst the other won't. The problem occurs when you square it the second time. You're trying to solve

although when you square it, you lose the negative on the RHS, so you could also be trying to solve

and you'll find that the incorrect solution you get at the end is actually the solution to this, not the one with the negative on the RHS.
This doesn't mean that squaring the equation is wrong, it just means that every time you square an equation to solve it, you need to check that your solutions solve the original equation. Though, you should generally be doing this regardless.
it's half a parabola flipped onto its side. It intersects with y = 3 once so there is only one solution when solving the equation.
However, when you square the second equation, you introduce a second solution. Why? The easiest way for me to show this is with an example. Take for example,
obviously this has one solution, namely, 1. Now, if you instead decided to go through a convoluted method of solving it, you could square it to get
There's a difference here. Both 1 and -1 now solve this equation, all because you squared it. It's essentially because you lost any information about the sign of each side of the equation when you squared it. You could just as easily square
and get the same result.
In the second question above, you will get two solutions. One of the solutions will satisfy the original equation, whilst the other won't. The problem occurs when you square it the second time. You're trying to solve
although when you square it, you lose the negative on the RHS, so you could also be trying to solve
and you'll find that the incorrect solution you get at the end is actually the solution to this, not the one with the negative on the RHS.
This doesn't mean that squaring the equation is wrong, it just means that every time you square an equation to solve it, you need to check that your solutions solve the original equation. Though, you should generally be doing this regardless.
Last edited:
zannasheayarrow
Member
Thank you all so much! I got the answers to both. And thank you for not just giving me the answers - this way I will actually learn how to do them 
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
A bit of a neat way of doing the second question more quickly is by drawing y=sqrt(x) and y=sqrt(3x+1) and then adding the graphs.
Then draw y=3 and you will easily see that there exists only one solution.
Since the expression is fairly simple, it can easily be seen by inspection that equality occurs when x=1.
Graphical argument ftw.
Then draw y=3 and you will easily see that there exists only one solution.
Since the expression is fairly simple, it can easily be seen by inspection that equality occurs when x=1.
Graphical argument ftw.