Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Help - Real Analysis
So I read somewhere that:
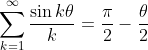
However they derived it some weird way that I know nothing about (this is STEP Advanced Problems #43)
Now I set out to derive this, I first though of integrating the sum of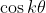
And I knew how to derive a closed formula for this sum, via:
}{1-z} )
And substituting z= cis theta in there, and equating real parts, then simplification. All that was easily done, then I had the task of integrating the beast.
I arrived at the result:
\theta + \cos n\theta -1}{4\cos^2 \frac{\theta}{2} } )
I do realise I need to take a limit for n to infinity, but I will hope to do that later, but I got stuck, I was able to get up to:
 \theta}{4\cos^2 \theta/2} \ d\theta + C )
I plugged in those integrals into Wolfram Alpha and it spat out something horrible so I am assuming I cannot find the exact definite integral for that.
But all I needed to do, was to find:
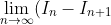 )
Where,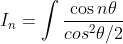
Question 1: The limit is all I need to find in order to complete this yes?
Now, I do know the IBP formula and I have done it just a couple of times, so I barely know anything from it, because I haven't done 4U Integration at school yet. But I have yet to be able to complete this problem, the final goal of it is to be able to show that:
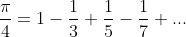
By utilising a substitution
Question 2: Can anyone give me guidance on how to do this using HSC techniques?
So I read somewhere that:
However they derived it some weird way that I know nothing about (this is STEP Advanced Problems #43)
Now I set out to derive this, I first though of integrating the sum of
And I knew how to derive a closed formula for this sum, via:
And substituting z= cis theta in there, and equating real parts, then simplification. All that was easily done, then I had the task of integrating the beast.
I arrived at the result:
I do realise I need to take a limit for n to infinity, but I will hope to do that later, but I got stuck, I was able to get up to:
I plugged in those integrals into Wolfram Alpha and it spat out something horrible so I am assuming I cannot find the exact definite integral for that.
But all I needed to do, was to find:
Where,
Question 1: The limit is all I need to find in order to complete this yes?
Now, I do know the IBP formula and I have done it just a couple of times, so I barely know anything from it, because I haven't done 4U Integration at school yet. But I have yet to be able to complete this problem, the final goal of it is to be able to show that:
By utilising a substitution
Question 2: Can anyone give me guidance on how to do this using HSC techniques?
Last edited:
