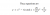b) Hence find the equations of any quadratics that pass through the origin and are tangent to both y= -2x - 4 and to y = 8x -49
I've never tried one like this but I'll give it a shot.
If the quadratic passes through the origin then y = ax<sup>2</sup> +bx + c, where c=0
y= -2x-4, gradient = -2 and y intercept = -4 (1)
y=8x -49, gradient = 8 and y intercept = -49 (2)
combining (1) with the expression obtained in 1.a) [y= c - (m-b)<sup>2</sup>/4a] but now where c=0
-4 = -(-2-b)<sup>2</sup>/4a ----> (b+2)<sup>2</sup>/4 = 4a (3)
combining (2) with the expression obtained in a)
-49 = -(8-b)<sup>2</sup>/4a ----> (8-b)<sup>2</sup>/49 = 4a (4)
Using (3) and (4)
(b+2)<sup>2</sup>/4 = (8-b)<sup>2</sup>/49
(b+2)/2 = (8-b)/7
(here I'm slightly unsure about where to take ± so I'll just take one. If someone could correct me on this and show me the convention that'd be cool.)
±7(b+2) = 16 - 2b
either b = 2/9 or b=-6
using (b+2)<sup>2</sup> = 4a
16 = 16a ---> a =1 when b=-6 -----> quadratic y = x<sup>2</sup> -6x
using b=2/9 seems to give something that isn't an answer. ^ There's one of them in any case.