1) Prove, for all positive integers 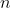 , the identity
, the identity
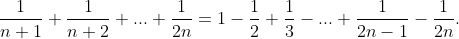
2) The sequence is given by
is given by  and
and  for
for 
a) Prove by induction that for ,
,  ) , where
, where 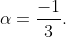
b) Hence find the limiting value of as
as 
3) A sequence is defined by ) where
where  and
and 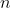 is a positive integer.
is a positive integer.
a) Use induction to show that^ \big(2^{n-1}\big) ) (the 2^n-1 is the power of the adjacent of fraction)
(the 2^n-1 is the power of the adjacent of fraction)
b) Hence find the limiting value of as
as 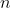 becomes large.
becomes large.
Any help would greatly be appreciated!
2) The sequence
a) Prove by induction that for
b) Hence find the limiting value of
3) A sequence is defined by
a) Use induction to show that
b) Hence find the limiting value of
Any help would greatly be appreciated!
