I was asked to expand on my comments with a more detailed answer, so here goes:
Part (a)
} \\ \\ \text{Let $x = \frac{p}{q}$, where $p$ and $q$ are coprime and $pq \neq 0$, be a root of} \qquad ax^3 - 3x + b &= 0 \qquad \text{where $a$, $b \in \mathbb{Z}$} \\ a\left(\frac{p}{q}\right)^3 - 3\left(\frac{p}{q}\right) + b &= 0 \\ \frac{ap^3}{q^3} - \frac{3p}{q} + b &= 0 \\ ap^3 - 3pq^2 + bq^3 &= 0 \\ \\ \text{This statement may be expressed as} \qquad ap^3 &= 3pq^2 - bq^3 = q^2(3p - bq) \quad \quad \text{. . . . . (1)} \\ \text{Or, alternatively, as} \qquad bq^3 &= 3pq^2 - ap^3 = p(3q^2 - ap^2) \quad \quad \text{. . . . . (2)} \end{align*})
Now,
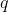
is clearly a factor of the RHS of statement (1), and so must also be a factor of
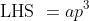
. However, with
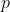
and
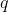
being coprime (and so sharing no factors other than
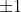
, it follows that either
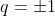
or
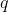
is a factor of

. In either case,
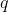
divides

.
Similarly,
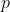
is clearly a factor of the RHS of statement (2), and so must also be a factor of
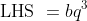
. However, with
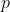
and
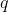
being coprime (and so sharing no factors other than
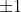
, it follows that either
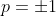
or
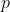
is a factor of
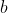
. In either case,
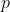
divides
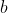
.
The equation (*) is the same equation with
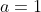
and
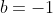
. For this equation to have a rational root requires
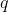
divides
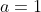
and
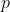
divides
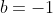
or that they are
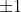
. In other words, the only possible rational roots of (*) are
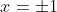
. However:
:} \qquad \text{LHS} &= x^3 - 3x - 1 = 1^3 - 3(1) - 1 = 1 - 3 - 1 = -3 \neq 0 \qquad \implies \qquad x = 1\ \text{is not a root of (*)} \\ \text{Test $x = -1$ in (*):} \qquad \text{LHS} &= x^3 - 3x - 1 = (-1)^3 - 3(-1) - 1 = -1 + 3 - 1 = 1 \neq 0 \quad \implies \quad x = -1\ \text{is not a root of (*)} \end{align*})
Hence, the equation (*) has no rational roots.
Part (b)
:} \qquad \left(r + s\sqrt{d}\right)^3 - 3\left(r + s\sqrt{d}\right) - 1 &= 0 \qquad \text{where $r$, $s$, and $d \in \mathbb{Q}$ but $\sqrt{d} \notin \mathbb{Q}$} \\ r^3 + 3r^2s\sqrt{d} + 3r\left(s\sqrt{d}\right)^2 + \left(s\sqrt{d}\right)^3 -3r - 3s\sqrt{d} - 1 &= 0 \\ r^3 + 3r^2s\sqrt{d} + 3rs^2d + s^3d\sqrt{d} - 3r - 3s\sqrt{d} - 1 &= 0 \\ \left(r^3 + 3rs^2d - 3r - 1\right) + s\sqrt{d}\left(3r^2 + s^2d - 3\right) &= 0 \\ \text{Since $\sqrt{d} \notin \mathbb{Q}$ and thus $d \neq 0$, this can only be true if} \qquad s\sqrt{d}\left(3r^2 + s^2d - 3\right) &= 0 \\ 3r^2s + s^3d - 3s &= 0 \qquad \text{as required} \end{align*})
In fact, since
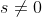
(as that would make the root being tested rational, which is impossible from part (a)), we have actually shown that
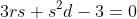
, and also that
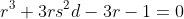
.
Testing
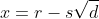
will yield
 - s\sqrt{d}\left(3r^2 + s^2d - 3\right) = 0)
using these results, confirming that it must also be a root.
Knowing that two of the roots are
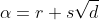
and
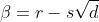
and setting the third root to
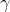
, it follows that
 + \left(r - s\sqrt{d}\right) + \gamma &= 0 \\ \gamma = -2r \end{align*})
but this makes the third root rational, which is impossible by part (a), and so there can be no root of the form
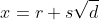
.

