Q13... You have the function
 = |ax + b|)
(a) From the given graph, you know at least two points that satisfy the function,
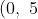)
and
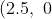)
. Using the first point:
 &= 5 \\ |a \times 0 + b| &= 5 \\ |b| &= 5 \\ b &= \pm 5 \end{align*})
and using the second point,
 &= 0 \\ |a \times 2.5 + b| &= 0 \\ |2.5a + b| &= 0 \\ 2.5a + b &= 0 \\ 5a + 2b &= 0 \\ 5a &= -2b \\ \text{Now, since $b = \pm5$, } 5a &= -2 \times \pm 5 = \mp 10 \\ a &= \mp 2 \end{align*})
So, we have two possible solutions:
Possibility 1: 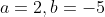
which leads to
 = |2x - 5|) Possibility 2:
Possibility 2: 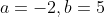
which leads to
 = |-2x + 5|)
But these are the same, as
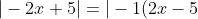| = |-1| \times |2x - 5| = 1 \times |2x - 5| = |2x - 5|)
So, both solutions are valid. The solutions on the exam are flawed, however, in that they find
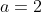
by starting with
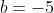
without first establishing the value of

.
Part (b) requires you to solve
 \ge 3)
. The solution will be the same whichever of the previous solutions you choose as they both result in the same
)
and so have the same equation to solve,
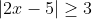
. This can be solved by cases:
Case 1: 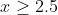
, in which case
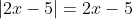
and so

and this solution is valid throughout the restricted domain
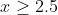
.
Case 2: 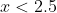
, in which case
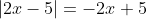
as
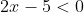
and so

and this solution is valid throughout the restricted domain
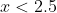
.
So, the complete solution of
 \ge 3)
is
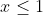
or
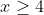
. This can be expressed in interval notation as
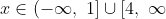)
.
Part (b) can also be solved graphically by adding the line
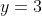
to the given diagram, noting that there are intersections at
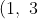)
and
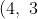)
, and then recognising that
 \ge 3)
when the given graph lies above the line that you have added. The solution
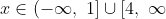)
immediately follows.

