themoonspretty
New Member
- Joined
- Sep 1, 2013
- Messages
- 13
- Gender
- Male
- HSC
- N/A
Re: HSC 2013 4U Marathon
Prove the volume of sphere
Prove the volume of sphere
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
O yep hehftfy
A lot of the inequalities I post here I take directly from the books:Do you guys have the book in which you got these questions from? Thanks.
Using double angle formula:
Yep that's it, well done.Using double angle formula:
sin(x)=2cos(x/2)sin(x/2)
=2cos(x/2)[2sin(x/4)cos(x/4)]
=..........
This process is repeated till the nth term so
sin(x)=2^n [cos(x/2)cos(x/4)....cos(x/2^n)]sin(x/2^n)
Divide both sides by x
sin(x)/x=[cos(x/2)cos(x/4)....cos(x/2^n)]sin(x/2^n)/x/2^n
As n-->infinity sin(x/2^n)/x/2^n-->1
So we get
sin(x)/x=cos(x/2)cos(x/4)....
For lim n-->infinity
ii) I'm guessing we sub x=pi/2 then play around with it?
We know that:
The biggest part is really just intuition lol. The fact that all the powers are even (Holy shit, would have never gotten that. RealiseNothing, can you discuss you logic as to how you approach inequality questions.
Well done.We know that:
Now letand
Multiply both sides by 3 to establish the inequality:
Now consider:
Split the RHS up into the following:
Now using the inequality we establish before, we get:
Let this be A:
Hence since
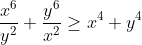
Any takers?
Yep. So it'd just beMultiply them?
Yeah that's what I was going forYep. So it'd just be.
I hope this is what sy was asking for..
Clearly that function is even, so we've checked that both plus or minus a_i is accounted for.
Can be solved by squaring all sides and doing tricks like changing aYeah that's what I was going for
This inequality is a good one, it had me stumped for a while:
 \left(\frac{3}{4} \right ) \dots \left(\frac{2n-1}{2n} \right ) < \frac{1}{\sqrt{2n}} )
Yep that is the method that I had done.Can be solved by squaring all sides and doing tricks like changing ato
to make it bigger/smaller as appropriate.
Something you mightn't have noticed about the expression in the middle is that it is actually equal to
which is actually a binomial coefficient (sorry i dont know the tex for them!). However also,is the total number of subsets of
, while the binomial coefficient is the total number of
element subsets. In other words, the expression in the middle is the probability a random subset of a 2n-element set has size exactly n.
The result just proven in the question says that... as n gets larger, this probability is bounded between constant multiples of. I.e. we have an *asymptotic growth estimate*.
So here's a new question which might be great to think about: can you prove using combinatorial / counting / probability estimates (and not savvy algebraic manipulation) that this is true?

