Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2013 MX2 Marathon (archive) (1 Viewer)
- Thread starter Sy123
- Start date
- Status
- Not open for further replies.
bleakarcher
Active Member
- Joined
- Jul 8, 2011
- Messages
- 1,502
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
Let z=cis(w_j).
=> cis(w_j)+[cis(w_j)]^2+...+[cis(w_j)]^n=cis(w_j)[[cis(w_j)]^n-1]/(z-1)
i.e. cis(w_j)+cis(2w_j)+...+cis(nw_j)=cis(w_j)[cis(nw_j)-1]/(z-1) by de Moivre's theorem
=cis(w_j)[cis(n[2pi*j/n])-1]/(z-1)=0
=> sum from t=1 to n [cos(tw_j)]=sum from t=1 to n [sin(tw_j)]=0, equating real and imaginary parts.
a) z+z^2+...+z^n=z[z^n-1]/(z-1)
Let z=cis(w_j).
=> cis(w_j)+[cis(w_j)]^2+...+[cis(w_j)]^n=cis(w_j)[[cis(w_j)]^n-1]/(z-1)
i.e. cis(w_j)+cis(2w_j)+...+cis(nw_j)=cis(w_j)[cis(nw_j)-1]/(z-1) by de Moivre's theorem
=cis(w_j)[cis(n[2pi*j/n])-1]/(z-1)=0
=> sum from t=1 to n [cos(tw_j)]=sum from t=1 to n [sin(tw_j)]=0, equating real and imaginary parts.
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon

If we fix j, we can still put it into alpha and it will still be a root since 'jk' will cover all the possible roots. Hence a general term of the nth roots of unity can be

Look at the sum of roots:

Write all of these roots in mod-arg form:
+ i\sum_{t=1}^{n} \sin(t\frac{2\pi j}{n}) )
Equate real and imaginary parts we arrive at the result:
= \sum_{t=0}^n \cos(tw_j) = 0 )
b)
For part i, note the identity that we can derive:
+\cos(A-B)=\cos A \cos B )
Apply to the result in part i:
 + \cos (t(w_j-w_k) )


+\cos(tw_p) = 0 )
Do things very similar for part ii except with
0.5(cos(A-B)-cos(A+B))
And in part iii
0.5(sin(A+B)+sin(A-B))
(x^{11}+x^{10}+...+x^2+x+\frac{90}{a}) )
Equate co-efficient of x

a=10, a=-9
Note the nth roots of unity. Lets call a general kth one of the nth roots of the unity:
If we fix j, we can still put it into alpha and it will still be a root since 'jk' will cover all the possible roots. Hence a general term of the nth roots of unity can be
Look at the sum of roots:
Write all of these roots in mod-arg form:
Equate real and imaginary parts we arrive at the result:
b)
For part i, note the identity that we can derive:
Apply to the result in part i:
Do things very similar for part ii except with
0.5(cos(A-B)-cos(A+B))
And in part iii
0.5(sin(A+B)+sin(A-B))
Is it a=3, b=2? (just need to check before I post my answer)
Equate co-efficient of x
a=10, a=-9
HeroicPandas
Heroic!
- Joined
- Mar 8, 2012
- Messages
- 1,545
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
Were u chasing for zzconj = |z|^2 to make use of |z|=1?(1-z)(1+z) / (1+z)(1+z)
If |z|=1, the numerator is imaginary, the denominator is real
so the real part of the fraction is zero.
HeroicPandas
Heroic!
- Joined
- Mar 8, 2012
- Messages
- 1,545
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
 Show this information on a sketch.} \\\text{b) Explain why there are positive real numbers k, L so that kz = 0.5(a + b)})
 = 0.5a - b})
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
 )

Now, the point R lies on both vectors. Indeed for OM, it lies on the vector therefore there must exist some real constant k such that we reduce the modulus of
Such that it equals to
Similarly, QN is \vec{ON}-b. And R lies on this line, hence there exists some constant L such that we reduce the modulus by such a factor to make L(z-b)=0.5a-b
===================
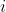 $Given that $ \ \ z=\cos \theta + i\sin \theta \ \ $Show that$ \ \ z^n + z^{-n} \ \ $ is real for positive integers n$ )
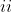 $Hence or otherwise solve the equation$ \ \ \ 2z^4+3z^3+5z^2+3z+2=0 )
b) On our sketch, notice that:
Now, the point R lies on both vectors. Indeed for OM, it lies on the vector therefore there must exist some real constant k such that we reduce the modulus of
Such that it equals to
Similarly, QN is \vec{ON}-b. And R lies on this line, hence there exists some constant L such that we reduce the modulus by such a factor to make L(z-b)=0.5a-b
===================
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
Although they are reciprocals of the question I asked, the result still applies.
We can prove that if they have modulus 1 (which u, v, w all do when solving the equation), then they are all purely imaginary, hence they all are collinear.
Lets cheat and use the result from the previous question I asked.u, v and w are the roots of (sqrt2)z^3 = 1+i. Show that (1+u)/(1-u), (1+v)/(1-v) and (1+w)/(1-w) are collinear.
Although they are reciprocals of the question I asked, the result still applies.
We can prove that if they have modulus 1 (which u, v, w all do when solving the equation), then they are all purely imaginary, hence they all are collinear.
Re: HSC 2013 4U Marathon

which is equal to onesince  ? this is probably the wrong reasoning lol, do you have to split it up using the triangular inequality or something?
? this is probably the wrong reasoning lol, do you have to split it up using the triangular inequality or something?
edit: can you say the numerator is and the denominator is
and the denominator is  therefore they cancel out?
therefore they cancel out?
I need to sleep...
which is equal to one
edit: can you say the numerator is
I need to sleep...
Last edited:
Fus Ro Dah
Member
- Joined
- Dec 16, 2011
- Messages
- 247
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
 approach to observe that
approach to observe that  , and then substitute into P(z). We acquire a polynomial that is easy to prove has all complex roots but proving that they are purely imaginary is so long and tedious, may as well just solve P(z) and substitute all the values in. I can't immediately think of a shorter method at the moment.
, and then substitute into P(z). We acquire a polynomial that is easy to prove has all complex roots but proving that they are purely imaginary is so long and tedious, may as well just solve P(z) and substitute all the values in. I can't immediately think of a shorter method at the moment.
Normally would have taken the usualu, v and w are the roots of (sqrt2)z^3 = 1+i. Show that (1+u)/(1-u), (1+v)/(1-v) and (1+w)/(1-w) are collinear.
Construct vectors A, B, B*, AB* and AB*-1. We immediately observe two congruent triangles, where matching sides include |A-B| and |AB*-1| and hence the result.Hey guys, a short question. Pretty simple but i really liked it

seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: HSC 2013 4U Marathon
For jyu's question the polynomial equation is equivalent to taking the cube roots of a complex number of unit modulus. These three roots must lie on the unit circle.
But the map
sends the unit circle (excluding 1) to the imaginary axis. To see this, simply multiply the numerator and denominator of this fraction by the conjugate of the denominator and simplify.
This implies the the images of u,v,w under this transformation all lie on the imaginary axis.
For jyu's question the polynomial equation is equivalent to taking the cube roots of a complex number of unit modulus. These three roots must lie on the unit circle.
But the map
sends the unit circle (excluding 1) to the imaginary axis. To see this, simply multiply the numerator and denominator of this fraction by the conjugate of the denominator and simplify.
This implies the the images of u,v,w under this transformation all lie on the imaginary axis.
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Re: HSC 2013 4U Marathon
http://en.wikipedia.org/wiki/Möbius_transformation
Might want to read up on this.Normally would have taken the usualapproach to observe that
, and then substitute into P(z). We acquire a polynomial that is easy to prove has all complex roots but proving that they are purely imaginary is so long and tedious, may as well just solve P(z) and substitute all the values in. I can't immediately think of a shorter method at the moment.
http://en.wikipedia.org/wiki/Möbius_transformation
HeroicPandas
Heroic!
- Joined
- Mar 8, 2012
- Messages
- 1,545
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
very niceb) On our sketch, notice that:
Now, the point R lies on both vectors. Indeed for OM, it lies on the vector therefore there must exist some real constant k such that we reduce the modulus of
Such that it equals to
Similarly, QN is \vec{ON}-b. And R lies on this line, hence there exists some constant L such that we reduce the modulus by such a factor to make L(z-b)=0.5a-b
===================
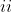 $Hence or otherwise solve the equation$ \ \ \ 2z^4+3z^3+5z^2+3z+2=0 )
Re: HSC 2013 4U Marathon
probably both
probably both
HeroicPandas
Heroic!
- Joined
- Mar 8, 2012
- Messages
- 1,545
- Gender
- Male
- HSC
- 2013
- Status
- Not open for further replies.
