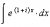I was playing around with these sorts of problems on the bus the other day, but I ended up confusing myself and didn't get very far.
Say you had a polynomial with roots
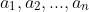
and you want to find a polynomial with roots
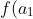, f(a_2), ..., f(a_n))
(Sy's question would be a special case of this where
 = x + \frac{1}{x})
).
You can find an
equation with these roots by replacing every instance of

in the polynomial with
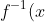)
(this is an interesting property to investigate/prove). In some cases, that equation can be algebraically manipulated into a polynomial without creating any new roots. This is why the trick of inverting coefficients works for
 = 1/x)
-- it's a shortcut to replacing all

terms with
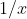
and multiplying out the resulting fractions.
When
)
isn't monotonic (meaning
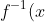)
is not a function), it still works; I'm pretty sure you can choose a maximal interval on its domain over which it's monotonic (probably the wrong terminology) and use that for the inverse, because the only necessity is that
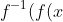) = x)
. Also, I'm not convinced that all equations generated in this manner can be manipulated into polynomials without creating new roots (for example, I had some trouble doing it with Sy's question, but I could have just messed up the algebra). Perhaps someone else will have more luck investigating this?