Re: HSC 2013 4U Marathon
dunno if it works lol

I probably made an error somewhere
ah, I did it without substitution by completing the square and converting to partial fractions. It should be able to be integated into inverse tans ?I don't think so, but I think its a bit unreasonable of me to ask it like that with no hint whatsoever.
Redone:
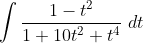
dunno if it works lol
I probably made an error somewhere
Last edited:



