-
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2013 MX2 Marathon (archive) (2 Viewers)
- Thread starter Sy123
- Start date
- Status
- Not open for further replies.
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
Wow I can't believe I went through all that and not notice that simple transformation...
Holy crap hahahaha you're rightLol sledgehammer.
Wow I can't believe I went through all that and not notice that simple transformation...
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Re: HSC 2013 4U Marathon
I noticed that in your code, you used {}^{m+n}C_m to denote nCr.
May I suggest that you can also use \binom{n}{r} to have the same effect?
^k) and then proving that
and then proving that 
Good solution.
Rearrangement gives required result.
I noticed that in your code, you used {}^{m+n}C_m to denote nCr.
May I suggest that you can also use \binom{n}{r} to have the same effect?
You can prove that the sequence is monotonically increasing by defining(I'm sure there is a more rigourous way to prove this inequality, I think it appeared in a HSC question before)
I think he meant for it to be proven algebraically, similarly to the classic "Prove e^pi > pi^e" problem.Um ... evaluate.
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon


Now, lets establish some approximations for e and pi.


Since this sum is increasing, therefore:

The only series for Pi that I know that could be used to approximate Pi is an alternating series which I will have a hard time proving that Pi is greater than it.
So: Consider a regular 12 gon inscribed within a circle of radius 1. It is possible to find the exact form of the area of the 12 gon which I know is less than the area of the circle:
Finding area of hte triangles and multiplying by 12, we get:
> \frac{1}{2} \left(\frac{3}{8} + \frac{1}{3} \right ) = \frac{17}{48} > \frac{17}{51} = \frac{1}{3} )
 > \frac{1}{3} )

EDIT: Nope nope nope I have to find Pi and e as the lower bound. Redoing.
Now, lets establish some approximations for e and pi.
Since this sum is increasing, therefore:
The only series for Pi that I know that could be used to approximate Pi is an alternating series which I will have a hard time proving that Pi is greater than it.
So: Consider a regular 12 gon inscribed within a circle of radius 1. It is possible to find the exact form of the area of the 12 gon which I know is less than the area of the circle:
Finding area of hte triangles and multiplying by 12, we get:
EDIT: Nope nope nope I have to find Pi and e as the lower bound. Redoing.
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: HSC 2013 4U Marathon
Regarding the approximation of pi by an alternating series:
Note that the series zig-zags by progressively smaller amounts. In fact we have every partial sum with an odd number of terms as an upper bound and every partial sum with an even number of terms as a lower bound. Moreover, the more terms we use the tighter these bounds are.
Regarding the approximation of pi by an alternating series:
Note that the series zig-zags by progressively smaller amounts. In fact we have every partial sum with an odd number of terms as an upper bound and every partial sum with an even number of terms as a lower bound. Moreover, the more terms we use the tighter these bounds are.
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
I can find upper bounds for pi and e using primitive methods but they are too weak, and I end up getting something lower than 1/3 :/
I was able to get e < 3 using trapezium and integral of e^x from 0 to 1.
And pi < 4 using a circle inscribed in a hexagon. But these approximations are too weak.
The approximations need to be quite strong as well since: \doteq 0.34 )
So the approximations need to be such that we sort for an error of 10^{-2} ....
So yeah I think we would have to rely on the formal series for pi and e to get a really accurate approximation, because I tried things like integration and even geometry but they aren't good enough.
Also, is there a series for e which we can use to get an upper bound for it? Because the lower bound won't work when we flip it.
Interesting, is there a direct way of proving this without computing pi/4 whatsoever?Regarding the approximation of pi by an alternating series:
Note that the series zig-zags by progressively smaller amounts. In fact we have every partial sum with an odd number of terms as an upper bound and every partial sum with an even number of terms as a lower bound. Moreover, the more terms we use the tighter these bounds are.
I can find upper bounds for pi and e using primitive methods but they are too weak, and I end up getting something lower than 1/3 :/
I was able to get e < 3 using trapezium and integral of e^x from 0 to 1.
And pi < 4 using a circle inscribed in a hexagon. But these approximations are too weak.
The approximations need to be quite strong as well since:
So the approximations need to be such that we sort for an error of 10^{-2} ....
So yeah I think we would have to rely on the formal series for pi and e to get a really accurate approximation, because I tried things like integration and even geometry but they aren't good enough.
Also, is there a series for e which we can use to get an upper bound for it? Because the lower bound won't work when we flip it.
HeroicPandas
Heroic!
- Joined
- Mar 8, 2012
- Messages
- 1,545
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
nvm i thought pi and e on the calculator were exact...
nvm i thought pi and e on the calculator were exact...
Last edited:
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: HSC 2013 4U Marathon
So you need series approximations with bounds on error.
For e, we have:
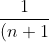!}<e-\sum_{k=0}^n \frac{1}{k!}<\frac{1}{n\cdot n!})
this is pretty easy to prove by induction, if we define e by the infinite series you mentioned.
Unfortunately, the Gregory series for pi is terrible, it takes ages to get anywhere near accurate. You would be better off by circumscribing and inscribing regular k-gons by the unit circle (k=12 might be nice if k=6 isn't good enough) and comparing areas to get surdic estimates, which are much easier to compare to 1/3.
Yep, by proving that all partial sums taking more terms are greater/less than our partial sum, do this by pairing adjacent terms and noting that the sequence is decreasing in size.Interesting, is there a direct way of proving this without computing pi/4 whatsoever?
I can find upper bounds for pi and e using primitive methods but they are too weak, and I end up getting something lower than 1/3 :/
I was able to get e < 3 using trapezium and integral of e^x from 0 to 1.
And pi < 4 using a circle inscribed in a hexagon. But these approximations are too weak.
The approximations need to be quite strong as well since:
So the approximations need to be such that we sort for an error of 10^{-2} ....
So yeah I think we would have to rely on the formal series for pi and e to get a really accurate approximation, because I tried things like integration and even geometry but they aren't good enough.
Also, is there a series for e which we can use to get an upper bound for it? Because the lower bound won't work when we flip it.
So you need series approximations with bounds on error.
For e, we have:
this is pretty easy to prove by induction, if we define e by the infinite series you mentioned.
Unfortunately, the Gregory series for pi is terrible, it takes ages to get anywhere near accurate. You would be better off by circumscribing and inscribing regular k-gons by the unit circle (k=12 might be nice if k=6 isn't good enough) and comparing areas to get surdic estimates, which are much easier to compare to 1/3.
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
So, we can establish a fairly accurate bound for e:
 using the inequality you made above.
using the inequality you made above.
Then I guess we could use:
^4}{1+x^2} = \frac{22}{7} - \pi )
Since that function is always positive then:


The use of 22/7 is a little cheaty, but the use of k-gons won't give a good enough approximation despite the one for e giving a great one.
In order to get an upper bound for pi, I need to consider inscribing a circle into the k-gon, and the only way I can do that and still have nice angles is k=6, since I need to split the 6 quadrilaterals in half in order to find the area.
Proof is then complete.
Ah ok I see.Yep, by proving that all partial sums taking more terms are greater/less than our partial sum, do this by pairing adjacent terms and noting that the sequence is decreasing in size.
So you need series approximations with bounds on error.
For e, we have:
this is pretty easy to prove by induction, if we define e by the infinite series you mentioned.
Unfortunately, the Gregory series for pi is terrible, it takes ages to get anywhere near accurate. You would be better off by circumscribing and inscribing regular k-gons by the unit circle (k=12 might be nice if k=6 isn't good enough) and comparing areas to get surdic estimates, which are much easier to compare to 1/3.
So, we can establish a fairly accurate bound for e:
Then I guess we could use:
Since that function is always positive then:
The use of 22/7 is a little cheaty, but the use of k-gons won't give a good enough approximation despite the one for e giving a great one.
In order to get an upper bound for pi, I need to consider inscribing a circle into the k-gon, and the only way I can do that and still have nice angles is k=6, since I need to split the 6 quadrilaterals in half in order to find the area.
Proof is then complete.
Last edited:
asianese
Σ
- Joined
- Sep 20, 2010
- Messages
- 2,219
- Gender
- Undisclosed
- HSC
- 2012
Re: HSC 2013 4U Marathon
 - they are merely symbolic representations - pi the ratio between the circumference and diameter, and e the base of the natural logarithm (among other interpretations). ANY form of the decimal approximations MUST be truncated at some point since the number is irrational and will have an infinite number of decimals. Your calculator uses series to approximate these constants: for e it uses
- they are merely symbolic representations - pi the ratio between the circumference and diameter, and e the base of the natural logarithm (among other interpretations). ANY form of the decimal approximations MUST be truncated at some point since the number is irrational and will have an infinite number of decimals. Your calculator uses series to approximate these constants: for e it uses  , truncating (stopping at a certain number) at n. And for
, truncating (stopping at a certain number) at n. And for ^k}{2k+1}\approx 4\sum_{k=0}^n \dfrac{(-1)^k}{2k+1}) , again truncating somewhere to give you enough accuracy.
, again truncating somewhere to give you enough accuracy.
No, in fact the only 'exact' forms of pi and e are exactly:nvm i thought pi and e on the calculator were exact...
Last edited:
HeroicPandas
Heroic!
- Joined
- Mar 8, 2012
- Messages
- 1,545
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
oh right thanks!No, in fact the only 'exact' forms of pi and e are exactly:- they are merely symbolic representations - pi the ratio between the circumference and diameter, and e the base of the natural logarithm (among other interpretations). ANY form of the decimal approximations MUST be truncated at some point since the number is irrational and will have an infinite number of decimals. Your calculator uses series to approximate these constants: for e it uses
, truncating (stopping at a certain number) at n. And for
, again truncating somewhere to give you enough accuracy.
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
Consider the integral:
!} f^{(k)} (x-t) \ dt )
Integrating by parts:
} (x-t) )
}(x-t) \ dt )
!} dt )

} (x-t) |_0^x + I_{k+1} )
} (0) )
Taking the sum from k=1 to n on both sides, the left sum telescopes:
} (0) )
 \ dt = -f(x-t) |_0^x = -f(0) + f(x) )
 + f(x) - I_{n+1} = \sum_{k=1}^{n} \frac{x^k}{k!} f^{(k)} (0) )
=\sum_{k=0}^n \frac{x^kf^{(k)}(0)}{k!}+\int_0^x \frac{t^nf^{(n+1)}(x-t)}{n!}\, dt )
Great questionHere is a form of Taylor's theorem that can be easily proven by MX2 methods:
where
denotes the k-th derivative of f, and n is any non-negative integer.
Consider the integral:
Integrating by parts:
Taking the sum from k=1 to n on both sides, the left sum telescopes:
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
If you don't mind me expanding on this
 Using part (i), prove that$ )
^{n+1}}{n!}e \int_0^1 t^n e^{-t} \ dt \ \ \ \fbox{3} )


 Show that$ )

 Hence prove that$ )

 Prove by mathematical induction$ )
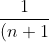!} < e - \sum_{k=0}^n \frac{1}{k!} < \frac{1}{n \cdot n!} \ \ \ \fbox{2} )


 Prove that$ )


 Hence prove that$ \ \ e \ \ $is irrational$ \ \ \ \ \fbox{2} )
If you don't mind me expanding on this
Here is a form of Taylor's theorem that can be easily proven by MX2 methods:
where
denotes the k-th derivative of f, and n is any non-negative integer.
Last edited:
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: HSC 2013 4U Marathon
The moral is that we can approximate smooth (or sufficiently differentiable) functions by polynomials, and the size of the error decays at the rate of a polynomial of degree one greater. (To see this note that each of the derivatives of f will be bounded in a small interval about 0, and bound the integral expression for the error using this).
One nice application of this is that if the difference between two sufficiently smooth functions is bounded by a constant times x^{n+1} (at least close to 0), then their first n derivatives at zero must be equal (try to see why this must be true). We say such a pair of functions are "equal up to order n". Eg sin(x) is equal to x up to order 1 about 0.
Another is that this gives us a quite intuitive way of proving the 0/0 form of L'Hospital's rule (try to see this also).
Yep, its one of my favourite elementary applications of IBP, Taylor's theorem is very important in many fields of mathematics.Great question
Consider the integral:
Integrating by parts:
Taking the sum from k=1 to n on both sides, the left sum telescopes:
=\sum_{k=0}^n \frac{x^kf^{(k)}(0)}{k!}+\int_0^x \frac{t^nf^{(n+1)}(x-t)}{n!}\, dt )
The moral is that we can approximate smooth (or sufficiently differentiable) functions by polynomials, and the size of the error decays at the rate of a polynomial of degree one greater. (To see this note that each of the derivatives of f will be bounded in a small interval about 0, and bound the integral expression for the error using this).
One nice application of this is that if the difference between two sufficiently smooth functions is bounded by a constant times x^{n+1} (at least close to 0), then their first n derivatives at zero must be equal (try to see why this must be true). We say such a pair of functions are "equal up to order n". Eg sin(x) is equal to x up to order 1 about 0.
Another is that this gives us a quite intuitive way of proving the 0/0 form of L'Hospital's rule (try to see this also).
- Status
- Not open for further replies.
