Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2013 MX2 Marathon (archive) (1 Viewer)
- Thread starter Sy123
- Start date
- Status
- Not open for further replies.
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: HSC 2013 4U Marathon
As no-one is answering spirals question I will give a solution for b). The rest is easy.
^n+(z-1)^n=0\Rightarrow (z+1)^n=-(z-1)^n\Rightarrow |z+1|^n=|z-1|^n\Rightarrow |z+1|=|z-1|.)
So any roots of this polynomial must lie on the perpendicular bisector of -1 and 1, that is the imaginary axis.
As no-one is answering spirals question I will give a solution for b). The rest is easy.
So any roots of this polynomial must lie on the perpendicular bisector of -1 and 1, that is the imaginary axis.
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
Is a_k real?Another question on polys/complex numbers:
:=\sum_{k=0}^n a_kz^k$ \\ \\has no complex roots $\alpha$ with $|\arg(\alpha)|\leq\pi/n.$ $)
RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 4U Marathon
yep totesDid you angle chase this too?
Re: HSC 2013 4U Marathon
)
RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 4U Marathon


Then the diagonals of the quadrilateral formed are:
 + (b+d)i)
 + (b-d)i)
Now multiply the gradients of the diagonals:

Suppose these diagonals intersect at right angles, hence:



But:


Hence:

Thus the quadrilateral formed is a rhombus if the diagonals intersect at right angles. Therefore the converse is true.
Let:
Then the diagonals of the quadrilateral formed are:
Now multiply the gradients of the diagonals:
Suppose these diagonals intersect at right angles, hence:
But:
Hence:
Thus the quadrilateral formed is a rhombus if the diagonals intersect at right angles. Therefore the converse is true.
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon


Now when we form the rhombus fixing one end at the origin, the diagonal coming from the origin will be z_1+z_2, and the other diagonal will be z_1-z_2.
Now lets see what we get when we take the argument of z_1+z_2 and z_1-z_2.
-arg(z_1-z_2) = k \\ \\ \tan^{-1} \frac{y+v}{x+u}-\tan^{-1} \frac{y-v}{x-u} = k \\ \\ \tan k = \frac{2vx-2uy}{x^2+y^2-u^2-v^2} )
That is after simplification, but notice


But this is unattainable, hence we can then deduce that k = pi/2, 3pi/2 etc.
Either way we have proven perpendicular property.
Is it mathematically legal for me to use this argument?
(Not a very elegant proof, I know, but is it possible for me to do this?)
Trying my best using complex numbers (otherwise its quite simple to prove that property, just prove that the 4 triangles that are created with diagonals of rhombus are all congruent)
Now when we form the rhombus fixing one end at the origin, the diagonal coming from the origin will be z_1+z_2, and the other diagonal will be z_1-z_2.
Now lets see what we get when we take the argument of z_1+z_2 and z_1-z_2.
That is after simplification, but notice
But this is unattainable, hence we can then deduce that k = pi/2, 3pi/2 etc.
Either way we have proven perpendicular property.
Is it mathematically legal for me to use this argument?
(Not a very elegant proof, I know, but is it possible for me to do this?)
Last edited:
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: HSC 2013 4U Marathon
Suppose to the contrary that a root alpha exists in this sector. Evaluating the polynomial P at this alpha we get a sum of (n+1) complex numbers which is supposedly equal to zero. Think about this sum geometrically and a problem should become pretty obvious. Its one of those things that may take a little while to spot, but when you see it you will slap yourself for not seeing it sooner .
.
If the above is not enough of a hint then try to do this problem for n=2 before attempting the general case.
At Sy's request a hint:Another question on polys/complex numbers:
:=\sum_{k=0}^n a_kz^k$ \\ \\has no complex roots $\alpha$ with $|\arg(\alpha)|\leq\pi/n.$ $)
Suppose to the contrary that a root alpha exists in this sector. Evaluating the polynomial P at this alpha we get a sum of (n+1) complex numbers which is supposedly equal to zero. Think about this sum geometrically and a problem should become pretty obvious. Its one of those things that may take a little while to spot, but when you see it you will slap yourself for not seeing it sooner
If the above is not enough of a hint then try to do this problem for n=2 before attempting the general case.
RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 4U Marathon
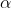 is a root of the polynomial.
is a root of the polynomial.
Let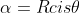 such that
such that 
Then by substituting this into our polynomial and letting it equal to 0 (since we are assuming it's a root) and by using De Moivre's Theorem, we obtain:
\theta + a_{n-1}R^{n-1}cis(n-1)\theta + ... + a_1Rcis\theta + a_0 = 0)
If we plotted these points on an Argand Diagram,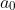 would be on the positive real axis given that
would be on the positive real axis given that 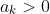 .
.
The leading term would lay in the first two quadrants, unless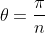 , in which case it would lay on the negative real axis.
, in which case it would lay on the negative real axis.
All terms in between would lay in the first two quadrants such that their imaginary components are positive.
By vector addition, since all points have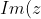 > 0) , we can never arrive at 0, and hence
, we can never arrive at 0, and hence 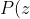 \neq 0)
Therefore we have a contradiction - our assumption is wrong. Hence we can deduce that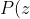) has no roots
has no roots 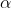 where
where | \leq \frac{\pi}{n})
Note by a symmetrical argument we can justify it holds true when all the points obey the condition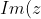 < 0) .
.
SupposeAnother question on polys/complex numbers:
:=\sum_{k=0}^n a_kz^k$ \\ \\has no complex roots $\alpha$ with $|\arg(\alpha)|\leq\pi/n.$ $)
Let
Then by substituting this into our polynomial and letting it equal to 0 (since we are assuming it's a root) and by using De Moivre's Theorem, we obtain:
If we plotted these points on an Argand Diagram,
The leading term would lay in the first two quadrants, unless
All terms in between would lay in the first two quadrants such that their imaginary components are positive.
By vector addition, since all points have
Therefore we have a contradiction - our assumption is wrong. Hence we can deduce that
Note by a symmetrical argument we can justify it holds true when all the points obey the condition
RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 4U Marathon
The Cauchy Schwarz Inequality can be proven like that as well yes? I remember carrot giving me that as a question at USYD when we went.Bingo. Nice result right? I will try to think of harder questions along these lines later.
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: HSC 2013 4U Marathon
I can't think of how off the top of my head, although there are pretty simple ways to visualise C-S geometrically...in many ways it is more fundamental than the triangle inequality. Was Carrot's question proving C-S for z,w in C^n? Or just in R^n?The Cauchy Schwarz Inequality can be proven like that as well yes? I remember carrot giving me that as a question at USYD when we went.
RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 4U Marathon
^2 \geq 0)
Which you can show by adding all the terms graphically.
Then use the discriminant and the inequality falls straight out.
(something like this, might not be the exact question).
It was showing thatI can't think of how off the top of my head, although there are pretty simple ways to visualise C-S geometrically...in many ways it is more fundamental than the triangle inequality. Was Carrot's question proving C-S for z,w in C^n? Or just in R^n?
Which you can show by adding all the terms graphically.
Then use the discriminant and the inequality falls straight out.
(something like this, might not be the exact question).
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: HSC 2013 4U Marathon
Well pretty different theme, everything is real here, and the inequality comes directly from squares being positive. But yeah, that is one of the common proofs for the real version of C-S.
Well pretty different theme, everything is real here, and the inequality comes directly from squares being positive. But yeah, that is one of the common proofs for the real version of C-S.
Re: HSC 2013 4U Marathon
$\\\therefore \arg\left ( \frac{{\overrightarrow{AB}}}{{\overrightarrow{AD}}} \right )+\arg\left ( \frac{{\overrightarrow{CB}}}{{\overrightarrow{CD}}} \right )=\pi \\\arg\left ( \frac{z_4-z_1}{z_2-z_1} \right )+\arg\left ( \frac{z_2-z_3}{z_4-z_3} \right )=\pi\\\arg\left ( \frac{(z_4-z_1)(z_2-z_3)}{(z_2-z_1)(z_4-z_3)} \right )=\pi\\ \frac{(z_4-z_1)(z_2-z_3)}{(z_2-z_1)(z_4-z_3)} \right )=-k, (k> 0)\\\therefore$ it is a negative real number$)
editing
Basic but because I cant think of any original questions at the moment and to keep the marathon going:
(z_2-z_3)}{(z_2-z_1)(z_4-z_3)} $ is a negative real number$ )
Last edited:
- Status
- Not open for further replies.

