Re: HSC 2013 3U Marathon Thread
haha oops, got mixed up between the threadsNah as in isn't this the 3U thread?
nvm
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
haha oops, got mixed up between the threadsNah as in isn't this the 3U thread?
nvm
Through drawing a diagram, we can see that the side of a square, s is given by:
Through drawing a diagram, we can see that the side of a square, s is given by:
Hence area of one square is: 4(r-y)^2
Volume thus by integrating from r to -r, i.e. from the top to the bottom, we get 32/3 r^3
Not quite, that might be its locus, but we don't know what alpha is (i.e. Re(z-i)/(z+1) = 0 )
Is this what you mean?
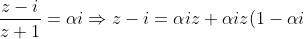 = \alpha i+i \Rightarrow z=i\dfrac{(\alpha+1)}{1-\alpha i}\cdot\dfrac{1+\alpha i}{1+\alpha i} \\ = i\dfrac{(\alpha+1)+i(\alpha^2+\alpha)}{1+\alpha^2} \\ = -\dfrac{\alpha^2+\alpha}{1+\alpha^2}+i\dfrac{\alpha+1}{1+\alpha^2}.)
Is everyone allowed to answer these questions?
Hint: Choose
yepAlso twinklegal, my explanation is wrong, the variable square is above the fixed square of units y, but still using similar triangles as we wake a triangle to the top of the thing, I still get the same answer :/
EDIT: NVM, we just take from O to a side of the square directly, then pythagoras theorem, to get sidelength 2sqrt(r^2-x^2), squaring this and integrating from -r to r we get 16r^3/3?
Dividing using long division, we get that:Hint: Chooseas the largest root(s) and consider the discriminant of

The numbers in pascal's triangle can be represented by binomial coefficients, the nth row and kth spot number is given by:Prove that four consecutive terms in a row of the Pascal triangle cannot form an AP.
Do you mean x and y instead of a and b inside the sum?
yep, cheers.Do you mean x and y instead of a and b inside the sum?
LetShow that, if the four points representing the complex numbers z1, z2, z3, z4 are concyclic, the fraction (z1-z2)(z3-z4)/(z3-z2)(z1-z4) must be real.
