Immortality
Rekt by Adv. English
- Joined
- Apr 15, 2014
- Messages
- 108
- Gender
- Male
- HSC
- 2014
Re: HSC 2014 4U Marathon
Sketch the locus of z on an Argand Diagram of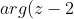 + arg(z+2) = \pi )
Sketch the locus of z on an Argand Diagram of
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
This is not entirely correct. Think about domain/range restrictions!I'm not sure if this is right (haven't touched complex in a while)
arg(z-2)+arg(z+2)=pi
arg((z-2)(z+2))=pi
arg(z^2-4)=pi
Thus, the complex number z^2-4 must be purely real
Let z=x+iy
z^2-4 = (x^2-y^2-4)+2ixy
Demand: Im(z)=0
2xy=0
xy=0
Pair of intersecting lines (x=0 ; y=0)
very good (Y)View attachment 30306?, chat is bugged
Inequality signs like < need a space before/after so that everything shows up.View attachment 30306?, chat is bugged
The equation shows symmetry in x and y. Interchanging x and y yields the same equation, the inverse is the same relation.Curve sketching, don't hate <a href="http://www.codecogs.com/eqnedit.php?latex=Sketch\,\,&space;the\,\,&space;curve\,\,&space;x^2&space;-9xy+y^2&space;=1" target="_blank"><img src="http://latex.codecogs.com/gif.latex?Sketch\,\,&space;the\,\,&space;curve\,\,&space;x^2&space;-9xy+y^2&space;=1" title="Sketch\,\, the\,\, curve\,\, x^2 -9xy+y^2 =1" /></a>
unnecessary use of latex
Other than converting x^2/a^2 - y^2/b^2 =1 to xy=c^2, rotating entire curves is not in the course.The equation shows symmetry in x and y. Interchanging x and y yields the same equation, the inverse is the same relation.
Rotate the relation by 45 deg anticlockwise, the new relation will be symmetrical about the y-axis.
Sketch the new relation 11x^2/2 -7y^2/2=1, a hyperbola.
Rotate the hyperbola by 45 deg clockwise to obtain the graph of x^2-9xy+y^2=1
You can use complex numbers to obtain a formula for rotations at an MX2 level.Other than converting x^2/a^2 - y^2/b^2 =1 to xy=c^2, rotating entire curves is not in the course.
Just checking - how did you rotate the curve? Not using matrices I hope?
Just differentiate implicitly and go from there.
There is no mention of that in the syllabus - it is just the way that all textbooks have chosen to "prove that the hyperbola with equation xy=(1/2)a^2 is the hyperbola x^2 - y^2 = a^2 referred to different axes."You can use complex numbers to obtain a formula for rotations at an MX2 level.
You can think of rotating a curve as rotating an infinitely large set of points that happen to lie along some curve.There is no mention of that in the syllabus - it is just the way that all textbooks have chosen to "prove that the hyperbola with equation xy=(1/2)a^2 is the hyperbola x^2 - y^2 = a^2 referred to different axes."
Rotating points using complex number is one thing - rotating whole curves is something else.Other than converting x^2/a^2 - y^2/b^2 =1 to xy=c^2, rotating entire curves is not in the course.
Just checking - how did you rotate the curve? Not using matrices I hope?
Just differentiate implicitly and go from there.
Not that I think it is a difficult concept to get across, but I am quite confident that if this was ever to appear in an HSC exam, there would be a LOT of hand-holding. For example, the algebra needed to eliminate the parameters in this particular question (although it appears in textbooks) would not be asked in an exam without a lead-in.
