FrankXie
Active Member
Re: HSC 2014 4U Marathon
for part (ii):
\cos\theta]^n )
Because the modulus of common ratio is less than 1, the limiting sum exists and
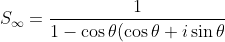})
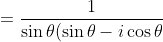})
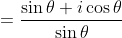
Finally equate the real part of both sides.
for part (ii):
Because the modulus of common ratio is less than 1, the limiting sum exists and
Finally equate the real part of both sides.
Last edited:

