Re: MX2 2015 Integration Marathon
Just wondering what is the point of defining a principal square root in the first place?
It's probably done so that there is a meaning to what is referred to by the expression
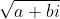
that mathematicians can agree on, which is probably useful in complex analysis, like how it's useful with real numbers. If we didn't have principal square roots for positive real numbers, we'd have to keep saying which one we're referring to if we were using one in an equation or something, whereas with a principal root defined, we don't need to do this. This may also be useful for complex numbers for those doing complex analysis.
Why should one take precedence over the other, especially when the choice seems completely arbitrary?
Well, for square roots of positive numbers, it's more natural to define the positive square root as the principal value. Otherwise, we'd have
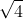
referring to -2 and
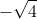
refer to +2. While there wouldn't be anything mathematically wrong with this (it's just notation), it's more natural and less confusing to have the notation that has a negative sign to be the negative number, so we define the principal value of the square root of a positive number as the positive square root.
Defining the principal value of a complex number as the one with positive real part is maybe done because then the definition of the principal value of the square root of a positive real number is consistent with this, so the complex number definition works for all complex numbers except for the negative real numbers (since these have square roots with 0 real part). For a negative number
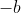
, maybe the principal square root is taken to be
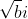
(where
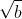
refers to the principal value, which is the positive square root), since
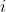
is defined as the principal value of
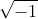
.
