Re: HSC 2015 4U Marathon - Advanced Level
I would like to propose my own solution to the lines-in-a-plane problem. It's a simple two-case interpretation, which I hope it's comprehensive.
Looking at our definitions, we know that parallel lines never meet in a plane. Any one
non-parallel line, therefore, will meet all other lines of similar nature, once within the plane. These intersections can be shared by two or more lines, but if any one line does not share an intersection with any other line within the plane, it must intersect it once elsewhere.
We start off with 2 non-parallel lines, introducing our first intersection to the plane. From here, the minimum number of added intersections with the next line would be 0, by sharing the first intersection with the other lines. However, since we have to exclude at least 1 line from the common intersection, our last line would have to intersect all others once.
If at any point before the last line (let's say, at the rth line, where 1 < r < n) we decide not to share the initial intersection with previous lines, our first deviant line would have to intersect with all other lines once at separate points, adding r-1 intersections to the plane. After this first digression, we know that there is no point on the plane shared by all lines. That is, there is no one point on the plane where lines after the rth line will intersect with all other lines at once. At the very least, therefore, all lines after this will add 1 new intersection to the plane. This is the best case scenario, where we keep adding lines to the intersection shared by the r-1 lines from before (ensuring that each new line intersects with all other lines except for the rth one, which it will have to intersect at a separate point).
Compare the two cases:
(1) where we share the initial intersection until the last line, whereupon the sequence of added intersections will be
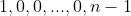
.
(2) where we introduce a new intersection anytime before the last line, whereupon the sequence would change to

at the very best.
Each sequence constitutes a set of n elements (for our n lines). Thus, in the first sequence, we have a total of 1+n-1 = n distinct intersections. In the second case, at the very least we have 1+r-1+(n-r)(1) = n distinct intersections.
Therefore, the absolute minimum number of distinct intersections throughout our plane is n.



