Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2015 MX2 Marathon (archive) (2 Viewers)
- Thread starter Trebla
- Start date
- Status
- Not open for further replies.
dan964
what
Re: HSC 2015 4U Marathon
(I) is fine. modulus is , argument is
, argument is  which I know you got based by the '...'
which I know you got based by the '...'
(II) is fine as well. As mentioned above by others, modulus is not needed.
tip: except in probability, 'and' usually implies '+'
correct method, yes
(I) is fine. modulus is
(II) is fine as well. As mentioned above by others, modulus is not needed.
tip: except in probability, 'and' usually implies '+'
Last edited:
dan964
what
Re: HSC 2015 4U Marathon
Lets say each had a perimeter of X. X>0. Therefore each side is X/n, n>2 n is an integer
(A) and (B) can be proven by inscribing each REGULAR polygon inside a circle
(A) Each side subtends an angle of 2pi/n at the centre, forming an isosceles triangle
(B) Producing perpendiculars at each side bisects each side, producing sides of X/(2n) and a centre angle of (pi/n)
Using trig. to find the perpendicular gives h=cot(pi/n)*X/2n
Each triangle is therefore has an area of X^2/4n^2*cot(pi/n)
There are n triangles: A = (X^2/4n)*cot(pi/n) is the area (*)
Step 2: Consider the limiting case
The limit of y/tan(y) as y approaches 0 is 1.
Let y be pi/n
cot(pi/n) *pi/n as pi/n approaches 0 is 1.
Therefore as n approaches infinity: cot(pi/n)*1/n equals 1/pi
Side Note: From (*)
Let n approach infinity (the limiting case, i.e. a circle) gives X^2/4pi (by substituting 2pi * r you get the formula)
Differentiate (*) to get
X^2/4n^3 * cosec^2(pi/n) - X^2/2n^3 * cot(pi/n)
X^2/4n^3 * (D+1)^2 where D is cot(pi/n)
which is positive for n>2.
Since the area is positive for n=3, and the dA/dn is positive, as n increases, so does A. So therefore when n is a max, A is a max. Therefore at n --> infinity, A approaches a maximum. (X^2/4pi)
etc.
Therefore circle has the largest area if PERIMETER is constant for all regular polygon.
Step 1: To produce a formula.
Lets say each had a perimeter of X. X>0. Therefore each side is X/n, n>2 n is an integer
(A) and (B) can be proven by inscribing each REGULAR polygon inside a circle
(A) Each side subtends an angle of 2pi/n at the centre, forming an isosceles triangle
(B) Producing perpendiculars at each side bisects each side, producing sides of X/(2n) and a centre angle of (pi/n)
Using trig. to find the perpendicular gives h=cot(pi/n)*X/2n
Each triangle is therefore has an area of X^2/4n^2*cot(pi/n)
There are n triangles: A = (X^2/4n)*cot(pi/n) is the area (*)
Step 2: Consider the limiting case
The limit of y/tan(y) as y approaches 0 is 1.
Let y be pi/n
cot(pi/n) *pi/n as pi/n approaches 0 is 1.
Therefore as n approaches infinity: cot(pi/n)*1/n equals 1/pi
Side Note: From (*)
Let n approach infinity (the limiting case, i.e. a circle) gives X^2/4pi (by substituting 2pi * r you get the formula)
Differentiate (*) to get
X^2/4n^3 * cosec^2(pi/n) - X^2/2n^3 * cot(pi/n)
X^2/4n^3 * (D+1)^2 where D is cot(pi/n)
which is positive for n>2.
Since the area is positive for n=3, and the dA/dn is positive, as n increases, so does A. So therefore when n is a max, A is a max. Therefore at n --> infinity, A approaches a maximum. (X^2/4pi)
etc.
Therefore circle has the largest area if PERIMETER is constant for all regular polygon.
Last edited:
Re: HSC 2015 4U Marathon
I couldn't find what this was referring to. Would you explain what you mean in the non-probabilistic sense, perhaps with an example or two.tip: except in probability, 'and' usually implies '+'
dan964
what
Re: HSC 2015 4U Marathon
I understood what he meant, but felt like writing a note.
https://www.google.com.au/#q=3+and+4+equals
or the classic joke of 9 and 10 gives 21 (actually 19 but whatever)
It was a general note, in response to an earlier usage (of which was straightforward)I couldn't find what this was referring to.
I understood what he meant, but felt like writing a note.
3 and 4 give 7 not 12.Would you explain what you mean in the non-probabilistic sense, perhaps with an example or two.
https://www.google.com.au/#q=3+and+4+equals
or the classic joke of 9 and 10 gives 21 (actually 19 but whatever)
Last edited:
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2015 4U Marathon
Yes well done, for the other users who attempted this question (your attempt was deleted in a site crash yesterday), the key part I was looking for is what I boldedStep 1: To produce a formula.
Lets say each had a perimeter of X. X>0. Therefore each side is X/n, n>2 n is an integer
(A) and (B) can be proven by inscribing each REGULAR polygon inside a circle
(A) Each side subtends an angle of 2pi/n at the centre, forming an isosceles triangle
(B) Producing perpendiculars at each side bisects each side, producing sides of X/(2n) and a centre angle of (pi/n)
Using trig. to find the perpendicular gives h=cot(pi/n)*X/2n
Each triangle is therefore has an area of X^2/4n^2*cot(pi/n)
There are n triangles: A = (X^2/4n)*cot(pi/n) is the area (*)
Step 2: Consider the limiting case
The limit of y/tan(y) as y approaches 0 is 1.
Let y be pi/n
cot(pi/n) *pi/n as pi/n approaches 0 is 1.
Therefore as n approaches infinity: cot(pi/n)*1/n equals 1/pi
Side Note: From (*)
Let n approach infinity (the limiting case, i.e. a circle) gives X^2/4pi (by substituting 2pi * r you get the formula)
Differentiate (*) to get
X^2/4n^3 * cosec^2(pi/n) - X^2/2n^3 * cot(pi/n)
X^2/4n^3 * (D+1)^2 where D is cot(pi/n)
which is positive for n>2.
Since the area is positive for n=3, and the dA/dn is positive, as n increases, so does A. So therefore when n is a max, A is a max. Therefore at n --> infinity, A approaches a maximum. (X^2/4pi)
etc.
Therefore circle has the largest area if PERIMETER is constant for all regular polygon.
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Re: HSC 2015 4U Marathon
does circle geometry work for conics? I know it says circle but surely conics have some rules as well?
does circle geometry work for conics? I know it says circle but surely conics have some rules as well?
Re: HSC 2015 4U Marathon
Those 'rules' .... they are all those things you've derived in doing all those Conics questions.does circle geometry work for conics? I know it says circle but surely conics have some rules as well?
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Re: HSC 2015 4U Marathon
Oh that makes sense ahahahahahahh can you write the formulas that are assumed knowledge ?Those 'rules' .... they are all those things you've derived in doing all those Conics questions.
Ekman
Well-Known Member
- Joined
- Oct 23, 2014
- Messages
- 1,614
- Gender
- Male
- HSC
- 2015
Ekman
Well-Known Member
- Joined
- Oct 23, 2014
- Messages
- 1,614
- Gender
- Male
- HSC
- 2015
Re: HSC 2015 4U Marathon
 $ (u+v)(\bar{u} + \bar{v}) = |u+v|^2 )
(\bar{u} + \bar{v}) = |u|^2+|v|^2 +u\bar{v} +\bar{u}v = |u|^2+|v|^2 + uv \left(\frac{\bar{u}}{u} + \frac{\bar{v}}{v} \right))
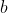 $ |x_k - P| = Px_k $ (This is the modulus of the vector of $ PX_k $ )$ )
^2 = |x_k|^2 + |-p|^2 -p\bar{x_k} -\bar{p}x_k $ (Using part a) )$)
^2 = \sum_{k=0}^{n-1} |x_k|^2 + |-p|^2 -p\bar{x_k} -\bar{p}x_k )


^2 = 2n )
------------------------------------------------
$ )
Last edited:
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2015 4U Marathon
Yep that is correct, your explanation for why those extra terms cancel out is a little vague, but that's the general idea
Ekman
Well-Known Member
- Joined
- Oct 23, 2014
- Messages
- 1,614
- Gender
- Male
- HSC
- 2015
Re: HSC 2015 4U Marathon
I would of drew an Argand diagram to demonstrate the cancelling out process.Yep that is correct, your explanation for why those extra terms cancel out is a little vague, but that's the general idea
Ekman
Well-Known Member
- Joined
- Oct 23, 2014
- Messages
- 1,614
- Gender
- Male
- HSC
- 2015
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2015 4U Marathon
) = \sum_{k=0}^{n-1} 2 - \sum_{k=0}^{n-1}(p\bar{x_k} + \bar{p} x_k) = 2n - p\sum_{k=0}^{n-1}\bar{x_k} - \bar{p} \sum_{k=0}^{n-1} x_k = 2n - p \overline{\sum_{k=0}^{n-1} x_k} - \bar{p} \sum_{k=0}^{n-1} x_k \\ \\ \sum_{k=0}^{n-1} x_k = 0 \ $(sum of roots of$ \ x^n - 1 = 0 ) \\ \\ \therefore \ \sum_{k=0}^{n-1} PX_k^2 = 2n )
Right, a more rigorous way of showing it would be to do this:I would of drew an Argand diagram to demonstrate the cancelling out process.
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
- Status
- Not open for further replies.

