HSC 2015 MX2 Marathon (archive) (2 Viewers)

Sy123 · May 1, 2015

Re: HSC 2015 4U Marathon

Just an exercise in mathematical/logical argument and proof:

$\\ $You may assume that the addition of any 2 positive integers is a positive integer$$

$\\ $i) Prove that the subtraction between any 2 positive integers is not always a positive integer$$

$\\ $ii) Prove that the addition or subtraction between any 2 integers is an integer$

$\\ $iii) Prove that the addition or subtraction between any 2 rational numbers is a rational number$

$\\ $iv) Prove that the addition of an irrational number and a rational number is always an irrational number$

Sy123 · May 1, 2015

Re: HSC 2015 4U Marathon

$\\ $Consider the sequence of polynomials defined by$ \\ \\ 1) \ C_0(x) = 1 \\ 2) \ C_1(x) = x \\ 3) \ C_n(x) = 2xC_{n-1}(x) - C_{n-2}(x) , \ n \geq 2$

$\\ $i) Show that$ \ C_n(\cos \theta) = \cos n\theta$

$\\ $ii) Let$ \ f_n(x,t) = t^n C_n(x) $. Show that$ \ f_n(x,t) = 2xt f_{n-1}(x,t) - t^2 f_{n-2}(x,t)$

$\\ $iii) Show that$ \ \sum_{n=0}^\infty C_n(x) t^n = \frac{1 - xt}{1-2xt + t^2}$

$\\ $iv) Hence find the value of$ \ \sum_{n=0}^{\infty} \frac{\cos \left(\frac{\pi}{8}n \right)}{2^n}$

Axio · May 3, 2015

Re: HSC 2015 4U Marathon

Sy123 said:
$\\ $Consider the sequence of polynomials defined by$ \\ \\ 1) \ C_0(x) = 1 \\ 2) \ C_1(x) = x \\ 3) \ C_n(x) = 2xC_{n-1}(x) - C_{n-2}(x) , \ n \geq 2$

$\\ $i) Show that$ \ C_n(\cos \theta) = \cos n\theta$

$\\ $ii) Let$ \ f_n(x,t) = t^n C_n(x) $. Show that$ \ f_n(x,t) = 2xt f_{n-1}(x,t) - t^2 f_{n-2}(x,t)$

$\\ $iii) Show that$ \ \sum_{n=0}^\infty C_n(x) t^n = \frac{1 - xt}{1-2xt + t^2}$

$\\ $iv) Hence find the value of$ \ \sum_{n=0}^{\infty} \frac{\cos \left(\frac{\pi}{8}n \right)}{2^n}$

Hey Sy could you maybe give a few hints for this question? I can only get part ii)...

glittergal96 · May 4, 2015

Re: HSC 2015 4U Marathon

Sy123 said:
Just an exercise in mathematical/logical argument and proof:

$\\ $You may assume that the addition of any 2 positive integers is a positive integer$$

$\\ $i) Prove that the subtraction between any 2 positive integers is not always a positive integer$$

$\\ $ii) Prove that the addition or subtraction between any 2 integers is an integer$

$\\ $iii) Prove that the addition or subtraction between any 2 rational numbers is a rational number$

$\\ $iv) Prove that the addition of an irrational number and a rational number is always an irrational number$

What exactly are you allowed to assume about addition/subtraction in i) and ii)? On which sets is it defined and what does it map pairs of elements from this set into? Just saying that the sum of two positive integers is a positive integer doesn't seem to be enough. (Given that we don't have a rigorous definition of the integers or +,- here.)

iii) and iv) are easy enough because we can define rational addition/subtraction/multiplication in terms of the corresponding operations on the integers, but since the definition of integers and the elementary operations on them is really fundamental (close to the axiomatic base), I think you need to be clearer about what we are allowed to assume.

glittergal96 · May 4, 2015

Re: HSC 2015 4U Marathon

Sy123 said:
$\\ $Consider the sequence of polynomials defined by$ \\ \\ 1) \ C_0(x) = 1 \\ 2) \ C_1(x) = x \\ 3) \ C_n(x) = 2xC_{n-1}(x) - C_{n-2}(x) , \ n \geq 2$

$\\ $i) Show that$ \ C_n(\cos \theta) = \cos n\theta$

$\\ $ii) Let$ \ f_n(x,t) = t^n C_n(x) $. Show that$ \ f_n(x,t) = 2xt f_{n-1}(x,t) - t^2 f_{n-2}(x,t)$

$\\ $iii) Show that$ \ \sum_{n=0}^\infty C_n(x) t^n = \frac{1 - xt}{1-2xt + t^2}$

$\\ $iv) Hence find the value of$ \ \sum_{n=0}^{\infty} \frac{\cos \left(\frac{\pi}{8}n \right)}{2^n}$

i) A straightforward induction. The key step:
$C_n(\cos(\theta))=2\cos(\theta)\cos((n-1)\theta)-\cos((n-2)\theta)\\ =(\cos(n\theta)+\cos((n-2)\theta))-\cos((n-2)\theta)=\cos(n\theta).$

ii) Directly replace each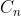 $C_n$ in the recurrence relation with $t^{-n}f_n$ and multiply out all negative powers of t.

iii) Lets introduce some additional assumptions so this thing converges. If $|x|\leq 1$ , then i) shows that $|C_n(x)|\leq 1$ for every non-negative integer n. If $|t|<1$ as well, then the sum is absolutely convergent by comparison with the series $\sum_n |t|^n.$ We proceed under this assumption as it is certainly sufficient for iv). (There IS value in studying these things as an algebraic object even if they don't converge though.)

$S:=\sum_{n=0}^\infty f_n = f_0+f_1 +\sum_{n=2}^\infty (2xtf_{n-1}-t^2f_{n-2})\\ = f_0+f_1 +2xt(S-f_0)-t^2S.$

Solving for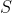 $S$ and using $f_0=1,f_1=xt$ completes the proof.

glittergal96 · May 4, 2015

Re: HSC 2015 4U Marathon

Oh I forgot iv).

Well just sub in
$x=\cos(\pi/8),t=1/2$
to the identity proven in iii).

You can also find a surdic expression for x if you are that way inclined, by using double angle formulae for example.

Chlee1998 · May 4, 2015

Re: HSC 2015 4U Marathon

glittergal96 said:
Oh I forgot iv).

Well just sub in
$x=\cos(\pi/8),t=1/2$
to the identity proven in iii).

You can also find a surdic expression for x if you are that way inclined, by using double angle formulae for example.

can you solve the questions in the current advanced thread?

glittergal96 · May 5, 2015

Re: HSC 2015 4U Marathon

Chlee1998 said:
can you solve the questions in the current advanced thread?

Oh, I didn't realise there were unanswered ones. I'll try them tomorrow.

Chlee1998 · May 5, 2015

Re: HSC 2015 4U Marathon

glittergal96 said:
Oh, I didn't realise there were unanswered ones. I'll try them tomorrow.

will be waiting

Axio · May 6, 2015

Re: HSC 2015 4U Marathon

$$Show that if n is a positive integer, then for all$ \ x>0:$

$x-\frac{x^2}{2}+\frac{x^3}{3}-...-\frac{x^{2n}}{2n}<ln(x+1)<x-\frac{x^2}{2}+\frac{x^3}{3}-...+\frac{x^{2n-1}}{2n-1}$

Sy123 · May 10, 2015

Re: HSC 2015 4U Marathon

$\\ $A solid has a circle of radius 1 as its base in a plane$ \ p \ $and every cross-section cut of the solid, perpendicular to the plane$ \ p $, is an equilateral triangle$ \\ \\ $Find the volume of the solid$$

Sy123 · May 10, 2015

Re: HSC 2015 4U Marathon

Axio said:
$$Show that if n is a positive integer, then for all$ \ x>0:$

$x-\frac{x^2}{2}+\frac{x^3}{3}-...-\frac{x^{2n}}{2n}<ln(x+1)<x-\frac{x^2}{2}+\frac{x^3}{3}-...+\frac{x^{2n-1}}{2n-1}$

$\\ 1 - x + x^2 - x^3 + \dots + (-1)^{2n-1}x^{2n-1} = \frac{1-x^{2n}}{1+x}$

$\\ 1 - x + x^2 - \dots + (-1)^{2n-2} x^{2n-2} = \frac{1 + x^{2n-1}}{1+x}$

$\\ (1): \ \ \int_0^z 1 - x + x^2 - x^3 + \dots + (-1)^{2n-1}x^{2n-1} \ \mathrm{d}x = \int_0^z\frac{1}{1+x} \ \mathrm{d}x - \int_0^z \frac{x^{2n}}{1+x} \ \mathrm{d}x$

$\\ (2): \ \ \int_0^z 1 - x + x^2 - \dots + (-1)^{2n-2} x^{2n-2} = \int_0^z\frac{1}{1+x} \ \mathrm{d}x + \int_0^z \frac{x^{2n-1}}{1+x} \ \mathrm{d}x$

$\\ (1): \Rightarrow \ z-\frac{z^2}{2}+\frac{z^3}{3}-...-\frac{z^{2n}}{2n} = \ln(z+1) - I_{2n}$

$\\ (2): \Rightarrow \ I_{2n-1} + \ln(z+1) = z-\frac{z^2}{2}+\frac{z^3}{3}-...+\frac{z^{2n-1}}{2n-1}$

$\\ $Where$ \ I_N = \int_0^z \frac{x^{N}}{1+x} \ \mathrm{d}{x}$

$\\ $Since$ \ x > 0 \ $so$ \ I_N > 0 \ $so$ \\ \\ z-\frac{z^2}{2}+\frac{z^3}{3}-...-\frac{z^{2n}}{2n} \ln(z+1) < z-\frac{z^2}{2}+\frac{z^3}{3}-...+\frac{z^{2n-1}}{2n-1}$

-------------------------------

Extending on the question:

$\\ $ii) Let$ \ J_n = \int_0^1 \frac{x^n}{1+x} \ $, show that$ \ 0 < J_n < \frac{1}{n+1}$

$\\ $iii) Hence, prove that$ \ \ln 2 = \lim_{N \to \infty} \sum_{j=0}^{N} \frac{(-1)^{j+1}}{j}$

braintic · May 11, 2015

Re: HSC 2015 4U Marathon

Sy123 said:
$\\ $A solid has a circle of radius 1 as its base in a plane$ \ p \ $and every cross-section cut of the solid, perpendicular to the plane$ \ p $, is an equilateral triangle$ \\ \\ $Find the volume of the solid$$

For anyone who wants to picture the solid:

(Not equilateral, but same idea)

Many people can't visualise the 'spine'. Others can't see that the curvature happens in only one dimension, like a cylinder.

swagswagyoloswag · May 11, 2015

Re: HSC 2015 4U Marathon

Sy123 said:
$\\ $A solid has a circle of radius 1 as its base in a plane$ \ p \ $and every cross-section cut of the solid, perpendicular to the plane$ \ p $, is an equilateral triangle$ \\ \\ $Find the volume of the solid$$

$\delta V = \frac{1}{2}(2x)(2x)sin(60)\delta y$

$\delta V = \frac{1}{2}(4x^{2})(\frac{\sqrt{3}}{2}) \delta y$

$\delta V = \sqrt{3}(1-y^{2}) \delta y$

$V = \int_{-1}^{1} \sqrt{3}(1-y^{2}) dy$

$V = 2\sqrt{3} \int_{0}^{1} 1 - y^{2} dy$

Axio · May 11, 2015

Re: HSC 2015 4U Marathon

Sy123 said:
-------------------------------

Extending on the question:

$\\ $ii) Let$ \ J_n = \int_0^1 \frac{x^n}{1+x} \ $, show that$ \ 0 < J_n < \frac{1}{n+1}$

$\\ $iii) Hence, prove that$ \ \ln 2 = \lim_{N \to \infty} \sum_{j=0}^{N} \frac{(-1)^{j+1}}{j}$

Can only do iii atm (my solution could be wrong...):

$\frac{x^n+1}{x+1}=1-x+x^2...+(-1)^{n-1}x^{n-1}$

$\therefore J_{n}=\int_{0}^{1}(1-x+x^2...+(-1)^{n-1}x^{n-1})dx-\int_{0}^{1}\frac{1}{x+1}$

$J_{n}=\sum_{j=1}^{N}\frac{(-1)^{j+1}}{j}-ln2$

$$Using the ii inequality, as N \rightarrow \infty , 0<J_{n}<0$

$\therefore J_{n}\rightarrow 0$

$\therefore 0=\lim_{N\rightarrow \infty }\sum_{j=1}^{N}\frac{(-1)^{j+1}}{j}-ln2$

As required.

InteGrand · May 11, 2015

Re: HSC 2015 4U Marathon

Sy123 said:
$\\ 1 - x + x^2 - x^3 + \dots + (-1)^{2n-1}x^{2n-1} = \frac{1-x^{2n}}{1+x}$

$\\ 1 - x + x^2 - \dots + (-1)^{2n-2} x^{2n-2} = \frac{1 + x^{2n-1}}{1+x}$

$\\ (1): \ \ \int_0^z 1 - x + x^2 - x^3 + \dots + (-1)^{2n-1}x^{2n-1} \ \mathrm{d}x = \int_0^z\frac{1}{1+x} \ \mathrm{d}x - \int_0^z \frac{x^{2n}}{1+x} \ \mathrm{d}x$

$\\ (2): \ \ \int_0^z 1 - x + x^2 - \dots + (-1)^{2n-2} x^{2n-2} = \int_0^z\frac{1}{1+x} \ \mathrm{d}x + \int_0^z \frac{x^{2n-1}}{1+x} \ \mathrm{d}x$

$\\ (1): \Rightarrow \ z-\frac{z^2}{2}+\frac{z^3}{3}-...-\frac{z^{2n}}{2n} = \ln(z+1) - I_{2n}$

$\\ (2): \Rightarrow \ I_{2n-1} + \ln(z+1) = z-\frac{z^2}{2}+\frac{z^3}{3}-...+\frac{z^{2n-1}}{2n-1}$

$\\ $Where$ \ I_N = \int_0^z \frac{x^{N}}{1+x} \ \mathrm{d}{x}$

$\\ $Since$ \ x > 0 \ $so$ \ I_N > 0 \ $so$ \\ \\ z-\frac{z^2}{2}+\frac{z^3}{3}-...-\frac{z^{2n}}{2n} \ln(z+1) < z-\frac{z^2}{2}+\frac{z^3}{3}-...+\frac{z^{2n-1}}{2n-1}$

-------------------------------

Extending on the question:

$\\ $ii) Let$ \ J_n = \int_0^1 \frac{x^n}{1+x} \ $, show that$ \ 0 < J_n < \frac{1}{n+1}$

$\\ $iii) Hence, prove that$ \ \ln 2 = \lim_{N \to \infty} \sum_{j=0}^{N} \frac{(-1)^{j+1}}{j}$

Part ii):

$0 < \frac{x^n}{1+x} < x^n$ for $x\in (0,1)$ .

$\therefore 0 < \int _0 ^1 \frac{x^n}{1+x}\text{ d}x<\int _0 ^1 x^n\text{ d}x$

$\Rightarrow 0 <J_n<\frac{1}{n+1}$

Drsoccerball · May 14, 2015

Re: HSC 2015 4U Marathon

Just squeeze theorem ?

Drsoccerball · May 16, 2015

Re: HSC 2015 4U Marathon

Mechanics questions?

leehuan · May 16, 2015

Re: HSC 2015 4U Marathon

Easy mechanics question from an HSC paper before you guys start confusing me again.

$A submarine of mass m is travelling underwater at maximum power, in which its engines are delivering a force of F. The water is exerting a resistive force proportional to the square of the velocity of the sumbarine.$

$$(i)Deduce that$ \frac { dv }{ dt } =\frac { 1 }{ m } \left( F-k{ v }^{ 2 } \right)$

$$(ii)The submarine increases its velocity from ${ v }_{ i }$ to ${ v }_{ f }$. If the distance travelled is $d$ during this time, show that: $\\ d=\frac { m }{ 2k } \ln { \left( \frac { F-k{ { v }_{ i } }^{ 2 } }{ F-k{ { v }_{ f } }^{ 2 } } \right) }$

Drsoccerball · May 16, 2015

Re: HSC 2015 4U Marathon

leehuan said:
Easy mechanics question from an HSC paper before you guys start confusing me again.

$A submarine of mass m is travelling underwater at maximum power, in which its engines are delivering a force of F. The water is exerting a resistive force proportional to the square of the velocity of the sumbarine.$

$$(i)Deduce that$ \frac { dv }{ dt } =\frac { 1 }{ m } \left( F-k{ v }^{ 2 } \right)$

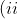$$(ii)The submarine increases its velocity from ${ v }_{ i }$ to ${ v }_{ f }$. If the distance travelled is $d$ during this time, show that: $\\ d=\frac { m }{ 2k } \ln { \left( \frac { F-k{ { v }_{ i } }^{ 2 } }{ F-k{ { v }_{ f } }^{ 2 } } \right) }$

i) $F=mg-kv^2$

$\therefore a= g- \frac{kv^2}{m}$

$\frac{dv}{dt}= g-\frac{kv^2}{m}$

$\frac{dv}{dt} = \frac{1}{m}(mg-kv^2)$

$\frac{dv}{dt} = \frac{1}{m}(F-kv^2)$

ii) $\frac{v \cdot dv}{dx} = \frac{gm-kv^2}{m}$

$\frac{dx}{dv}= \frac{mv}{gm-kv^2}$

$x= \frac{m}{2k}[ln(gm-kv^2)]_{v_f}^{v_i}$

$D= \frac{m}{2k}ln(\frac{F-kv^2_i}{F-kv^2_f})$

HSC 2015 MX2 Marathon (archive) (2 Viewers)

This too shall pass

This too shall pass

=o

Active Member

Active Member

Active Member

Member

Active Member

Member

=o

This too shall pass

This too shall pass

Well-Known Member

Member

=o

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Users Who Are Viewing This Thread (Users: 0, Guests: 2)