Re: HSC 2015 4U Marathon
NEXT QUESTION
Sorry, can't tell if the old one was finished.
http://imgur.com/k3Xgd2N
This was taken from the final page of my complex numbers test

It suffices to show all the results assuming
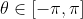
, due to the periodicity and powers of the functions in question. So assume
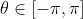
.
(i)
+i\sin \theta )
^2 + \sin^2 \theta})

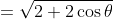
(since sin
2 t + cos
2 t = 1 ∀
t ∈ ℝ)
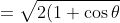})
.
If cos
θ ≠ -1, ℝe(1+
z) = 1+cos
θ > 1+(-1) = 0, so that
=\tan ^{-1}\left (\frac{\Im(1+z)}{\Re(1+z)} \right ))
)
)
, using the identity
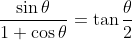
for cos
θ ≠ -1 (this can be proved using
t-formulae or half-angle identities)
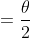
, since
)
, because we assumed that
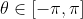
, and
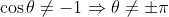
.
So for cos
θ ≠ -1,
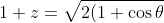}\left ( \cos\frac{\theta}{2}+i\sin\frac{\theta}{2} \right ) )
If cos
θ = -1 (that is, if
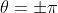
), then 1+
z = (1-1)+
i.sin(±π) = 0, and hence arg(1+
z) is undefined. However, the above formula still holds when 1+
z = 0 ⇔ cos
θ = -1.
So we have
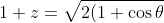}\left ( \cos\frac{\theta}{2}+i\sin\frac{\theta}{2} \right )\text{ }\forall \theta \in [-\pi,\pi] )
.
(ii) (1+
z)
4 = 1 + 4
z+6
z2 + 4
z3 +
z4, by the binomial theorem.
But by de Moivre's theorem and part (i),
^4=\left ( \sqrt{2(1+\cos\theta)}\right ) ^4\left ( \cos\frac{4\theta}{2}+i\sin\frac{4\theta}{2} \right ))
^4=4(1+\cos \theta)^2\left ( \cos2\theta+i\sin2\theta \right ))
^2 ( \cos2\theta+i\sin2\theta))
, since
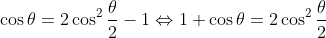
(from double angle identity for cosine)
)
.
Equating both expressions for (1+
z)
4,
)
The identity required to be shown follows from taking real parts of the above equation and recalling that by de Moivre's theorem,
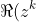=\cos k\theta )
and that 'real part' is a linear operator, so that the real part of a sum is the sum of real parts.
The second expression is given by
\sin 2\theta \text{ }\mathbf{(Equation \text{ }(\ast))})
, which follows in a similar way, this time by taking imaginary parts.
(iii)
The first identity follows by dividing Equation (*) by the identity required to prove in part (ii) (and recalling that
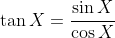
), for
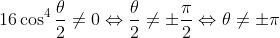
(so that the factor of
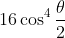
can be cancelled from the numerator and denominator).
For the second identity, we rearrange the identities proven in part (ii) to get:
\sin 2\theta - 6\sin 2\theta = \left ( 16\cos^4 \frac{\theta}{2} -6 \right )\sin 2\theta \text{ (1)})
and
\cos 2\theta - 6\cos2\theta = \left ( 16\cos^4 \frac{\theta}{2} -6 \right )\cos 2\theta \text{ (2)})
.
The identity follows upon dividing (1) by (2), provided that
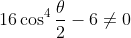
.

