FrankXie
Active Member
Re: HSC 2015 4U Marathon
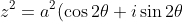, z^2+a^2=a^2[(1+\cos2\theta)+i\sin2\theta]=a^2(2\cos^2\theta+2i\sin\theta\cos\theta)=2a^2 \cos \theta (cos\theta+i\sin\theta), \therefore\quad\frac{z}{z^2+a^2}=\frac{a{\rm cis}\theta}{2a^2\cos\theta{\rm cis}\theta}=\frac{1}{2a\cos\theta} )
I knew that, just want more people get involved. here is my go:still left mine unanswered


