Re: HSC 2018 MX2 Marathon
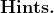

.$$)
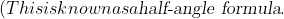 So to get $\cos^{4}x$, try squaring both sides of the above. You will need to use the half-angle formula once more to get to the final answer.$)
$)
$$)
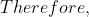
^{4} \\ &= \left(\frac{z + z^{-1}}{2}\right)^{4}\\ &= \ldots .\end{align*}$$)
$.$)
Find an expression for cos^4x in terms of cos4x and cos2x
Edit: The question is from terry lee so I'm guessing it implies that you use 4U complex techniques rather than 3U, I'm not sure if you can even use 3U for this...
