HSC Mathematics Marathon (3 Viewers)

apollo1 · Sep 24, 2011

im havin a go at largarithmic's question but here's another one in the mean time:

show that the polynomial:

$p(z) = z^{n}-z^{n-1}-1$

where $n\geq 2$ cannot have a repeated real root.

largarithmic · Sep 25, 2011

I go to sydney grammar

apollo1 said:
im havin a go at largarithmic's question but here's another one in the mean time:

show that the polynomial:

$p(z) = z^{n}-z^{n-1}-1$

where $n\geq 2$ cannot have a repeated real root.

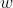Suppose it had a repeated root $w$ . Then taking the derivative, the following two are true:

$w^n - w^{n-1} = 1$
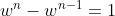
$nw^{n-1} - (n-1)w^{n-2} = 0$

Note eqn (1) implies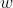 $w$ is nonzero. From that we can divide by 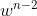$w^{n-2}$ in (2) to obtain:

$nw - (n-1) = 0$
$w = \frac{n-1}{n} < 1$

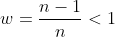
Now the problem with this is that if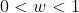 $0<w<1$ , then 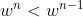$w^n < w^{n-1}$ which clearly contradicts the first equation. So it mustn't have had a repeated root in the first place. (messy question)

Here's a hard integration. Prove:

$\int_0^1 \frac{ln(1+x)}{1+x^2} dx = \frac{1}{8} \pi ln2$

apollo1 · Sep 25, 2011

largarithmic · Sep 25, 2011

yeah I initially forgot to end with [ /tex]

apollo1 · Sep 25, 2011

wat did u get for ur trial?

largarithmic · Sep 25, 2011

apollo1 said:
wat did u get for ur trial?

120

apollo1 · Sep 25, 2011

largarithmic said:
120

holy shit. i no whos gonna come first in the state for 4U this year. how about 3U wat did u get for that?

largarithmic · Sep 25, 2011

apollo1 said:
holy shit. i no whos gonna come first in the state for 4U this year. how about 3U wat did u get for that?

highly doubt ill come first, the grammar paper was really nice on me in particular and the markers were nice with some random oddities. got 83/84 for 3u

Alkanes · Sep 25, 2011

Beast.. Teach me please =D

apollo1 · Sep 25, 2011

largarithmic said:
highly doubt ill come first, the grammar paper was really nice on me in particular and the markers were nice with some random oddities. got 83/84 for 3u

m8 im willing to bet my life savings that you will come first.

Trebla · Sep 25, 2011

apollo1 said:
$\int_0^1 \frac{ln(1+x)}{1+x^2} dx = \frac{1}{8} \pi ln2$

Make the substitution x = tan u and then use the properties of definite integrals. I'll let someone else do it in full...

largarithmic · Sep 25, 2011

apollo1 said:
m8 im willing to bet my life savings that you will come first.

pretty poor bet lol. try horses instead. thanks for the encouragement though

Trebla said:
Make the substitution x = tan u and then use the properties of definite integrals. I'll let someone else do it in full...

yeah thats right, its a bit of a joke problem in a way coz its a bit unmotivatable after you do the trig sub (the usual neat solutions teachers have for it are just like, try this, magic it works). once youve done the trig sub you can do some other neat stuff though that is a bit more motivatable I think like use auxiliary angles but thats still hard

anyway time for a legitimate problem, but keep trying that polynomial thing. try this circle geo its neat

ABC is a triangle, and points D, E, F are chosen arbitrarily on each of sides BC, AC, AB. Let the circle through B,D,F meet the circle through C,D,E at G. Show the circle through A,E,F also goes through G

apollo1 · Sep 26, 2011

Trebla said:
Make the substitution x = tan u and then use the properties of definite integrals. I'll let someone else do it in full...

cool it worked

cutemouse · Sep 26, 2011

apollo1 said:
$\int_0^1 \frac{ln(1+x)}{1+x^2} dx = \frac{1}{8} \pi ln2$

What Trebla said and in addition Put cos theta + sin theta in the form R cos alpha and then using the symmtery property (ie. integral from 0 to a f(x) = integral from 0 to a f(a-x)) and then use log laws.

Btw, where did you get that question from?

largarithmic · Sep 26, 2011

cutemouse said:
What Trebla said and in addition Put cos theta + sin theta in the form R cos alpha and then using the symmtery property (ie. integral from 0 to a f(x) = integral from 0 to a f(a-x)) and then use log laws.

Btw, where did you get that question from?

yeah that

um it was in my 4u textbook. sydney grammar has its own textbook/handout that it hands out for 4u, apparently all the commercially available ones are crappy. They used to do that for 3u as well, until it got turned into the cambridge 3u book (pender, sadler, shea, ward are all current/former grammar teachers)

x_cp3 · Sep 26, 2011

What is it called ?

cutemouse · Sep 26, 2011

largarithmic said:
apparently all the commercially available ones are crappy.

They're not "crappy". They're just a bit irrelevant sometimes... Yeah if I was teaching 4U then I'd do that too.

K4M1N3 · Sep 26, 2011

largarithmic said:
ABC is a triangle, and points D, E, F are chosen arbitrarily on each of sides BC, AC, AB. Let the circle through B,D,F meet the circle through C,D,E at G. Show the circle through A,E,F also goes through G

$\angle cab + \angle abc + \angle bca = 180^o$ (1) (interior angle sum of triangle)
$\angle egd + \angle egf + \angle fgd = 360^o$ (2) (Angle sum at a point)
However since EGDC is a cyclic quad
$\angle egd = 180^o -\angle bca$ (3)
Similiarly for BDGF
$\angle fgd = 180^o -\angle abc$ (4)

Subbing 3 and 4 into 2

$\angle egf = \angle abc + \angle bca$

but from (1) $\angle abc + \angle bca = 180^o - \angle cab$

therefore $\angle egf = 180^o - \angle cab$

ie. angle egf and angle cab are supplmentary

therefore AEGF is a cyclic quad therefore the circle through A E and F must pass through G.

XD

largarithmic · Sep 26, 2011

x_cp3 said:
What is it called ?

"Sydney Grammar School, Mathematics Department, Extension 2 Exercises, 2011, Book One/Two". It's not even a real textbook, its a cheaply printed volume of notes and exercises with a light blue/light green (for book1/book2) cardboard cover.

And I think grammar thought the other textbooks were not challenging enough and didnt teach some of the topics in the way grammar wants to teach them. I dunn othough since Ive never used one

K4M1N3 said:
$\angle cab + \angle abc + \angle bca = 180^o$ (1) (interior angle sum of triangle)
$\angle egd + \angle egf + \angle fgd = 360^o$ (2) (Angle sum at a point)
However since EGDC is a cyclic quad
$\angle egd = 180^o -\angle bca$ (3)
Similiarly for BDGF
$\angle fgd = 180^o -\angle abc$ (4)

Subbing 3 and 4 into 2

$\angle egf = \angle abc + \angle bca$

but from (1) $\angle abc + \angle bca = 180^o - \angle cab$

therefore $\angle egf = 180^o - \angle cab$

ie. angle egf and angle cab are supplmentary

therefore AEGF is a cyclic quad therefore the circle through A E and F must pass through G.

XD

Thats right ^^ its a pretty neat result too, it's called "pivot theorem".

Anyway try this really nice probability question.

Alice and Bob take turns flipping a coin. Alice flips the coin N+1 times, and Bob flips it N times, where N is a positive integer. Alice 'wins' if she gets strictly more heads than Bob does. (e.g. if N=5 and Alice gets 4 heads 2 tails, while Bob gets 3 heads 2 tails, Alice wins; whereas if Bob got 4 heads 1 tail, she doesnt; and if he got all heads, he doesn't). Find the probability that Alice wins (in terms of N if necessary).

K4M1N3 · Sep 26, 2011

circle geo and now probability, how do you know my weaknesses......i vote hax!

HSC Mathematics Marathon (3 Viewers)

Banned

Member

Banned

Member

Banned

Member

Banned

Member

Active Member

Banned

Administrator

Member

Banned

Account Closed

Member

Member

Account Closed

Member

Member

Member

Users Who Are Viewing This Thread (Users: 0, Guests: 3)