When we discuss real-valued functions it's often convenient or more practical for us to take "continuous" to mean "continuous on
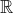
".
Most people accept this because whatever meaning we take is usually clear to the reader from context.
In this case it is (probably) not, so you should be more specific about what is meant for a function to be continuous or differentiable.
I agree with fan96, it is worth bearing in mind that
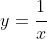
being continuous and differentiable throughout its domain
and that it has a discontinuity at
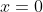
are not incompatible when considering continuity on
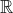
. Yes, there is an issue to be considered here when a question or statement is ambiguous, but don't let being
right in a technical sense get in the way of answering what is intended by a question, even if it is poorly expressed... and if necessary, include both answers.
Question: Is
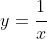
a continuous function?
Dangerous Answer: Yes
Dangerous Answer: No
Wiser Answer: Yes, it is continuous throughout its domain, which is
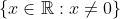
, but it does have a discontinuity at
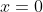
when considered over
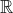
.

