Re: International Baccalaureate Maths Marathon
Just my opinion but comparing the IB Cambridge v HSC Cambridge (Yr 11/12 ) Extension books, the IB Cambridge is a far superior book. The book which is co-authored by 4 Cambridge University graduates, is written in a reader friendly way. I get comments from students that read the HSC Cambridge book and say it is too 'theoretical' and 'hard to understand' and I totally understand where they are coming from. You would think that be the opposite, with Cambridge Uni being a higher rank and the overall general consensus is a book written by Cambridge grads would be of higher mathematical literature.
I decided to do a bit of a comparison of the books:
WORKED EXAMPLES-
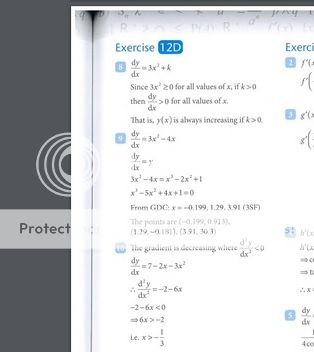
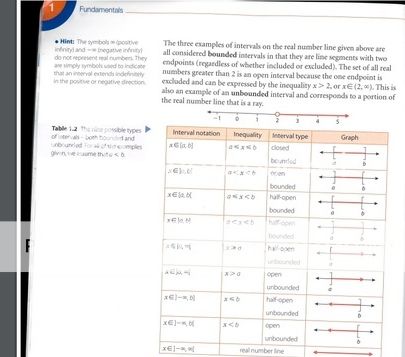
IB Cambridge- every step is explained in detail. With their graphs, they utilize different colours to break down key components. They keep things short and brief with their explanations.
HSC Cambridge- every example is black and yellow. Their explanations can be like essays sometimes.
EXPLANATION OF CONCEPTS:
IB Cambridge-Despite being 670 pages worth of content their explanations are brief and directly to the point. It's the kind of book where if you read a particular exercise it won't take you more longer than 5-15 minutes to understand what is going on, by just reading theory alone. They also include different colouring to emphasize their key points as well as bolded font to highlight some important formula. They give things like 'Exam Hints' and when linking it up to some history they keep it simple. They also provide an End of Chapter Review which goes through Key formula.
HSC Cambridge- It's a 637 page book but sometimes I feel its 6370 pages. Some exercises can go up to as much as 8 key points per exercise. I read chapter 8 of the Year 12 Cambridge and it seemed to me more of an English essay, personally feel they need to be more direct to the point and feel the need to make it more 'fun ' for the students to read. No end of chapter review summary is provided.
EXERCISES:
IB Cambridge- drill questions provide practice of new methods, they colour-code their questions to a certain IB Grade (i.e Band 4,5,6,7), questions predominantly exam-style
HSC Cambridge-breakdown is Basic, Development and Extension. Development questions are most similar to Exam style questions. Some of the exercises which have graphs, they use are hard-to-read background for the graphs.
AUTHORS:
IB Cambridge- Fannon, Kadelburg, Wooley, Stephen Ward are all Cambridge University graduates and teach both the IB and A Level Mathematics in the UK.
HSC Cambridge- Pender studied at Sydney University, Macquarie University & Bonn University. David Sadler - studied at Sydney Uni and UNSW. Julia Shea studied at University of Tasmania. David Ward studied at UNSW.
No offence to the universities in New South Wales or Australian universities but the Cambridge University maths school is better than any of the Australian University mathematics schools and the rankings prove this.