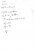member 6003
Member
- Joined
- Apr 20, 2022
- Messages
- 80
- Gender
- Male
- HSC
- 2023
Find the equation of the tangent to the parabola y=2x^2 at (1,2). Calculate its point of intersection with the x-axis and the volume of the solid formed when the area between the parabola, the tangent line and the x axis is revolved about the axis.
got a different answer, its apparently 2pi/3 for the volume
got a different answer, its apparently 2pi/3 for the volume