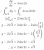Hey guys, there is a question about integration that I am having trouble with. It goes like this
A function has dy/dx= 4cos(2x) and passes through the point (pi/6, 2sqrt3). Find the exact equation of the function.
I know that y=2sin(2x) + C, but I don't know how to solve for C. Please help
A function has dy/dx= 4cos(2x) and passes through the point (pi/6, 2sqrt3). Find the exact equation of the function.
I know that y=2sin(2x) + C, but I don't know how to solve for C. Please help