Can someone help out with part d pls?
I have the solutions but idk what is happening and I want to know the thought process for solving it.
Okay there's the way you would solve it, and then there's many different ways you could think about it to get to that solution. I'm going to give you what I think (or have decided right now without proper thought) is the most intuitive way to understand it.
Our only information about the integrals (except for their actual definition, which is hard to solve) is a recurrence relation that they follow. There's a few things to observe:
1. Every time we go from
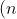I_{n-1})
to
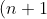I_{n})
, we
negate the original function and
add 2ln2. So if
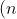I_{n-1})
had the term 2ln2, then it is negated and added back on so
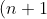I_{n})
won't have 2ln2 as a term. If
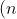I_{n-1})
didn't have a

, then it will be added so
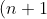I_{n})
will have this term. What that effectively means is that when going up the recursion ladder, 2ln2 is repeatedly added then removed, so it appears in every second integral. We see that in the recurrence relation so that's a good sign.
2. Initially,
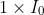
has the value
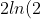-\frac{1}{1})
(from (i)). For now, let's just focus on that
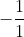
bit (as we already dealt with the 2ln2, but it's worth noting an even-indexed integral gives the 2ln2, so that's a good sign). Then to get to
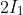
using the recurrence relation, we negate that and subtract

, getting us
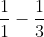
. Then to get to
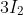
we do the same thing to get
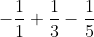
. Notice that we're slowly building the alternating series we see in the recurrence relation. Also note that the first term
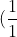)
always swaps sign, while the final term is always negative. Expanding the brackets in the recurrence relation, that's what we see so again that's a good sign.
That's pretty much all the pieces - it's much harder to say it than to think it and I'm sorry for my overly-wordy explanation. Once you've got that, it's just a matter of realising that mathematically - you could do induction twice in a few different ways (increasing by 2, as already suggested, or increasing by 1 and showing that it changes between the two different forms each time. The latter would require slightly more explanation). But the main thing is the logic, which I've tried to outline above.
Hope that helps - let me know if you've got more questions.