Interesting mathematical statements (1 Viewer)

[leehuan]

 

[Paradoxica]

that's not very interesting.

it's a fairly trivial consequence of Stirling's Approximation... and Limits...

 

[leehuan]

Too bad, cause even simple things like the power series for exp are interesting when you first see it.

(Also it was not a consequence in my homework. It was an intermediate step to GET to Stirling's approximation)

 

[Paradoxica]

Too bad, cause even simple things like the power series for exp are interesting when you first see it.

(Also it was not a consequence in my homework. It was an intermediate step to GET to Stirling's approximation)

I know. But I'm not the one doing it, so ¯\_(ツ)_/¯

 

[Sy123]

 

[sida1049]

It is as if you're trying to make our boys Uri and Daniel proud at the same time

 

[mrbunton]

the expression:
( (i0*(1*(1%(((i0 + 1) / (i1 + 1))+1))*(1%(((i0 + 1) / (i2 + 1))+1))*(1%(((i0 + 1) / (i3 + 1))+1))*(1%(((i0 + 1) / (i4 + 1))+1)))) + (i1*(1*(1%(((i1 + 1) / (i0 + 1))+1))*(1%(((i1 + 1) / (i2 + 1))+1))*(1%(((i1 + 1) / (i3 + 1))+1))*(1%(((i1 + 1) / (i4 + 1))+1)))) + (i2*(1*(1%(((i2 + 1) / (i0 + 1))+1))*(1%(((i2 + 1) / (i1 + 1))+1))*(1%(((i2 + 1) / (i3 + 1))+1))*(1%(((i2 + 1) / (i4 + 1))+1)))) + (i3*(1*(1%(((i3 + 1) / (i0 + 1))+1))*(1%(((i3 + 1) / (i1 + 1))+1))*(1%(((i3 + 1) / (i2 + 1))+1))*(1%(((i3 + 1) / (i4 + 1))+1)))) + (i4*(1*(1%(((i4 + 1) / (i0 + 1))+1))*(1%(((i4 + 1) / (i1 + 1))+1))*(1%(((i4 + 1) / (i2 + 1))+1))*(1%(((i4 + 1) / (i3 + 1))+1)))))/(0+1*(1%(((i0 + 1) / (i1 + 1))+1))*(1%(((i0 + 1) / (i2 + 1))+1))*(1%(((i0 + 1) / (i3 + 1))+1))*(1%(((i0 + 1) / (i4 + 1))+1))+1*(1%(((i1 + 1) / (i0 + 1))+1))*(1%(((i1 + 1) / (i2 + 1))+1))*(1%(((i1 + 1) / (i3 + 1))+1))*(1%(((i1 + 1) / (i4 + 1))+1))+1*(1%(((i2 + 1) / (i0 + 1))+1))*(1%(((i2 + 1) / (i1 + 1))+1))*(1%(((i2 + 1) / (i3 + 1))+1))*(1%(((i2 + 1) / (i4 + 1))+1))+1*(1%(((i3 + 1) / (i0 + 1))+1))*(1%(((i3 + 1) / (i1 + 1))+1))*(1%(((i3 + 1) / (i2 + 1))+1))*(1%(((i3 + 1) / (i4 + 1))+1))+1*(1%(((i4 + 1) / (i0 + 1))+1))*(1%(((i4 + 1) / (i1 + 1))+1))*(1%(((i4 + 1) / (i2 + 1))+1))*(1%(((i4 + 1) / (i3 + 1))+1)))

is equal to the largest positive integer(and 0) out of i0,i1,i2,i3,i4.
"a/b" denotes floor(a/b) or integer division
"a%b" denotes a mod b
"a+b" and "a*b" is obvious

generated through a python script. I realised that it's not the shortest way to express such a thing, but still. The most efficient expression would still take up acouple lines(i would think). I encourage other people to try to write an expression that is equal to the largest of two numbers using only these operations.

 

[fan96]

The principle of duality in the real projective plane is quite a beautiful result.
It's a stunning example of how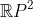 "removes the imperfections" from .

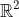(To put it informally, the real projective plane is the union of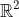 and a "line at infinity", with the property that parallel lines intersect on the "line at infinity".)

The principle of duality says that any theorem involving points and lines in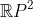 is still true if you replace "point" with "line" and vice versa.

And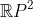 has more interesting properties, e.g. the fact that all non-degenerate conic sections are projectively equivalent.

 

[Arrowshaft]

for fast enough and .

 

[Drdusk]

for fast enough and .

Writing a and b is a crime in itself