-
Finished your HSC? Check out our University Discussion, Non-School forums or help out next year's HSC students! -
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
Interesting Q (1 Viewer)
- Thread starter zeebobDD
- Start date
try it
RealiseNothing
what is that?It is Cowpea
We know that 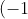^{x_j} $will always be 1 and$ (-1)^{y_i} $will always be -1$)
Because -1 to the power of an even is 1 and to the power of odd is -1.
So we can take any three at a time as a product, ie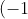^{x_1}(-1)^{y_1}(-1)^{x_2})
Now we want to add up all possible combinations of these. Let's split it up into 4 scenarios:
1) We choose 3 that are all even (xxx).
2) We choose 2 even and 1 odd (xxy).
3) We choose 1 even and 2 odd (xyy).
4) We choose 3 that are all odd (yyy).
Now let's work out what the answer will be if we were to randomly pick a combination from each group:
1) 3 evens = 1x1x1 = 1
2) 2 evens and 1 odd = 1x1x(-1) = -1
3) 1 even and 2 odd = 1x(-1)x(-1) = 1
4) 3 odds = (-1)x(-1)x(-1) = -1
Now let's find how many combinations we can have of each individual scenario:
1) We have 'p' amount of even integers and want to choose any 3, so it is
2) We have 2 'p' even integers and 1 'q' odd integer, so it is
3) We have 1 'p' and 2 'q', so it is
4) We have 3 'q', so it is
.
Now we want to sum all 4 scenarios up to find the total sum right? And we know that scenarios 1 and 3 are always equal to 1 and scenarios 2 and 4 are always equal to -1 since we showed that just before.
So the total sum is:
Put this into alegbraic form:
!3!} - \frac{p!q!}{(p-2)!(q-1)!2!1!} + \frac{p!q!}{(p-1)!(q-2)!2!1!} - \frac{q!}{(q-3)!3!})
Now since on the bottom of the first and last terms is a 3!, let's take out a 1/6, and then cancel out terms from top and bottom using stuff like!} = k)
Note that the ones with only 2! in the denominator will have to be multiplied by 3 to make up for factorising the 1/6:
(p-2) - 3(p)(p-1)(q) + 3(p)(q)(q-1) - q(q-1)(q-2)])
Expand the inside:
Now I'm going to just group together some terms and you will be able to see how we can further simplify from there, also notice how the -3pq and +3pq will cancel out in the above expression.
 - (3p^2 - 3q^2) + (2p - 2q)])
So now, notice how the first bracket is actually the binomial expansion for (p-q)^3.
Also, the second and third brackets can be factorised more, so:
^3 - 3(p^2 - q^2) + 2(p - q)])
Factor out a (p-q) from the bracket. Just note since p^2 - q^2 = (p-q)(p+q) due to a difference of two squares, when you factor out (p-q) you get (p+q) left over, hence:
[(p - q)^2 - 3(p + q) + 2])
QED.
Because -1 to the power of an even is 1 and to the power of odd is -1.
So we can take any three at a time as a product, ie
Now we want to add up all possible combinations of these. Let's split it up into 4 scenarios:
1) We choose 3 that are all even (xxx).
2) We choose 2 even and 1 odd (xxy).
3) We choose 1 even and 2 odd (xyy).
4) We choose 3 that are all odd (yyy).
Now let's work out what the answer will be if we were to randomly pick a combination from each group:
1) 3 evens = 1x1x1 = 1
2) 2 evens and 1 odd = 1x1x(-1) = -1
3) 1 even and 2 odd = 1x(-1)x(-1) = 1
4) 3 odds = (-1)x(-1)x(-1) = -1
Now let's find how many combinations we can have of each individual scenario:
1) We have 'p' amount of even integers and want to choose any 3, so it is
2) We have 2 'p' even integers and 1 'q' odd integer, so it is
3) We have 1 'p' and 2 'q', so it is
4) We have 3 'q', so it is
Now we want to sum all 4 scenarios up to find the total sum right? And we know that scenarios 1 and 3 are always equal to 1 and scenarios 2 and 4 are always equal to -1 since we showed that just before.
So the total sum is:
Put this into alegbraic form:
Now since on the bottom of the first and last terms is a 3!, let's take out a 1/6, and then cancel out terms from top and bottom using stuff like
Note that the ones with only 2! in the denominator will have to be multiplied by 3 to make up for factorising the 1/6:
Expand the inside:
Now I'm going to just group together some terms and you will be able to see how we can further simplify from there, also notice how the -3pq and +3pq will cancel out in the above expression.
So now, notice how the first bracket is actually the binomial expansion for (p-q)^3.
Also, the second and third brackets can be factorised more, so:
Factor out a (p-q) from the bracket. Just note since p^2 - q^2 = (p-q)(p+q) due to a difference of two squares, when you factor out (p-q) you get (p+q) left over, hence:
QED.
Last edited: