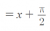Im really bad with my trig basics, i understand train of thought but could u explain how u converted -sinx into cosx+pi/2?
bc so - sinx = -cos(pi/2 - x)
and cos is even so fx = f-x
so say -cos(pi/2 - x) = f(-x)
and then im confused from here
We know that:
sin x = cos(pi/2 - x) #Note: This is one of the complementary angle there are 5 other identities(Use wikipedia if need be). The co in cosine means complementary. Similarly co has the same meaning with cot and cosec
=> -sin x = -cos(pi/2 -x)
=> sin(-x) = -cos(pi/2 - x) # -sin(x) = sin(-x) because sine is an odd function
=> sin(u) = -cos(pi/2 + u) # let u = -x
=> sin(x) = -cos(pi/2 + x) # Since u is dummy variable you can just replace it with x
=> -sin(x) = cos(pi/2 + x)
You can also apply the trick with u with function like sin(-3x+45) = -sin(3x-45) [This is because sine is odd].