ii) The line through
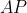
has equation
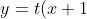 )
. (can you see why?)
Solve this simultaneously with the equation for the unit circle to obtain a quadratic in
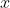
:
x^2+(2t^2)x+(t^2-1)=0)
This equation tells us where the line intersects the circle.
You could just throw the quadratic formula at this, but notice that one of the roots of this quadratic must be
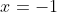
(because clearly the line passes through
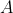
).
The product of roots is
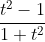
,
and so the other root must be
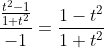
.
iii) We know
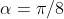
, and circle geometry tells us that
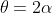
. So,
\right) = 1=\frac{2t}{1-t^2} )
and now you can easily solve for
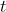
.
a)
 = \sin \arcsin x \cos \arccos x - \cos \arcsin x \sin \arccos x)

Because it is given that
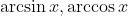
are acute, you can use the right triangle method.
Draw a right triangle with hypotenuse
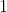
and sides
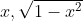
- then one of its angles is
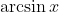
and the other is
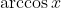
.
From this we see that

.
So we can show that
 \equiv x^2 - (1-x^2) \equiv 2x^2 -1 )
... for
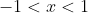
.
b) Similarly to a) you can draw another right triangle with sides
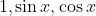
, but here's another way to do it.
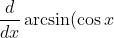) = \frac{-\sin x}{\sqrt{1-\cos^2x}} = -\frac{\sin x}{|\sin x|} = -1)
(as
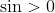
for acute angles)
Similarly,
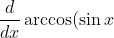) = -1 )
.
Therefore,
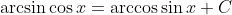
for some constant
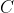
.
Set
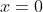
to show that
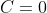
.
(With this method you can also show with little extra work that both expressions are identically equal to
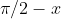
for acute

)