-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Inverse trig question (1 Viewer)
- Thread starter hs17
- Start date
Its always a good idea to state the domain for x before solving so:Solve the following equation
sin^-1 (x) - cos^-1 (x) = sin^-1 (3x+1)
Now take the sin of both sides to obtain:
Note that:
Therefore:
But
Last edited:
In case anyone does not see through why this part of the step is true:Its always a good idea to state the domain for x before solving so:and
.
Now take the sin of both sides to obtain:
Note that:and
by the pythagorean identities, we only have to take the positive case here since
Therefore:
Butso the only solution is:
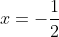
It's because of the domains of inverse trig functions.
Though that solution is a bit long lol.
Obviously:
Trivially, the equation is equivalent to:
Therefore,
Last edited:
fk latexIn case anyone does not see through why this part of the step is true:
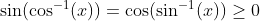
It's because of the domain's of inverse trig functions.
Though that solution is a bit long lol.
Obviously
[/TEX][/TEX]
You cant assumeIn case anyone does not see through why this part of the step is true:
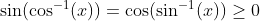
It's because of the domain's of inverse trig functions.
Though that solution is a bit long lol.
[/TEX]
trivialYou cant assumewithout proof. Nor can you assume
 = \cos^{-1} (3x+1) )
ahhh stupid latex good now i thinkfk latex
is this actually not assumable. it's so trivial.You cant assumewithout proof. Nor can you assume
 = \cos^{-1} (3x+1) )
If it’s not on the formula sheet you can’t assume it!is this actually not assumable. it's so trivial.
that's like all of 4u that you cant assume bruhIf it’s not on the formula sheet you can’t assume it!
Both results need the double angle formula which is similar to what I did so will result in the same length of working.is this actually not assumable. it's so trivial.
Only things you can assume are basic definitions and axioms and results that are on the data sheet (likethat's like all of 4u that you cant assume bruh
no just draw a triangle.Both results need the double angle formula which is similar to what I did so will result in the same length of working.
this is why real men take BOS Trials. Screw HSC.Only things you can assume are basic definitions and axioms and results that are on the data sheet (like)
Yeah u need double angle then 'draw a triangle,?' Proveno just draw a triangle.
bruh draw a triangle, its so obvious that sin inverse + cos inverse x = 90 degrees it's not even funny.Yeah u need double angle then 'draw a triangle,?' Provewithout double angle?
as for that:
pi/2 = inverse sin + inverse cos same thing.
- Joined
- Feb 16, 2005
- Messages
- 8,432
- Gender
- Male
- HSC
- 2006
FYI we mark the BoS trials in similar way to HSC lol. You can’t just assume results like that without proof, otherwise you can argue the result you’re trying to prove in the first place is also “trivial”.this is why real men take BOS Trials. Screw HSC.
ur trolling.FYI we mark the BoS trials in similar way to HSC lol. You can’t just assume results like that without proof, otherwise you can argue the result you’re trying to prove in the first place is also “trivial”.
inverse sin + inverse cos = pi/2 is like by definition basically.
is this assuming?
Daily struggles of a 4U kid....FYI we mark the BoS trials in similar way to HSC lol. You can’t just assume results like that without proof, otherwise you can argue the result you’re trying to prove in the first place is also “trivial”.
trying to write working out is harder than solving the question *sigh*Daily struggles of a 4U kid....
