-
Looking for HSC notes and resources? Check out our Notes & Resources page 
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
ITT we help examine to get 85 in his Maths extension 1 yearlies so he can do 4 unit (1 Viewer)
- Thread starter Examine
- Start date
deswa1
Well-Known Member
- Joined
- Jul 12, 2011
- Messages
- 2,251
- Gender
- Male
- HSC
- 2012
Re: ITT we help examine to get 85 in his Maths extension 1 yearlies so he can do 4 un
The instructions said you have to add "where he'll buy everyone a cookie". I'm not helping anymore...
Jokes- I'll do my best- post away
The instructions said you have to add "where he'll buy everyone a cookie". I'm not helping anymore...
Jokes- I'll do my best- post away
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Re: ITT we help examine to get 85 in his Maths extension 1 yearlies so he can do 4 un
No cookies.
No help.
No cookies.
No help.
Re: ITT we help examine to get 85 in his Maths extension 1 yearlies so he can do 4 un
Cookies mean peni* in hungarian lmaoNo cookies.
No help.
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Re: ITT we help examine to get 85 in his Maths extension 1 yearlies so he can do 4 un
Oh dear.
Oh dear.
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Re: ITT we help examine to get 85 in his Maths extension 1 yearlies so he can do 4 un
And by 'cookies', you mean the 'biscuit', right?
Ask away.
And by 'cookies', you mean the 'biscuit', right?
Ask away.
RealiseNothing
what is that?It is Cowpea
Re: ITT we help examine to get 85 in his Maths extension 1 yearlies so he can do 4 un
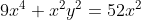
Solve the resulting quadratic.
For the second one, square the xy=8 to get (xy)^2 = 64. Then times the first equation by x^2 to getMy first questions
Solve simultaneously
7/x-5/y=3 and 2/x+25/2y=12
and
9x^2+y^2=52 and xy=8
Solve the resulting quadratic.
iBibah
Well-Known Member
- Joined
- Jun 13, 2012
- Messages
- 1,368
- Gender
- Male
- HSC
- 2013
Re: ITT we help examine to get 85 in his Maths extension 1 yearlies so he can do 4 un
&\frac{5}{y}=\frac{7}{x}-3\\&\frac{2}{x}+\frac{25}{2y}=12\\(2)&\frac{2}{x}+\left (\frac{5}{2}\cdot\frac{5}{y} \right )=12\\&Sub~ (1)~ in~ (2)\end{align*})
For the first one, make 5/y the subject for equation 1. Then sub into equation 2 because equation 2 is equal to 2/x+(5/2 x 5/y)=12. Solve for x then sub back in to equation 1 for y.My first questions
Solve simultaneously
7/x-5/y=3 and 2/x+25/2y=12
and
9x^2+y^2=52 and xy=8
Last edited:
Re: ITT we help examine to get 85 in his Maths extension 1 yearlies so he can do 4 un
I've reached this part, problem is I don't know how to solve it after this.For the second one, square the xy=8 to get (xy)^2 = 64. Then times the first equation by x^2 to get
Solve the resulting quadratic.
iBibah
Well-Known Member
- Joined
- Jun 13, 2012
- Messages
- 1,368
- Gender
- Male
- HSC
- 2013
Re: ITT we help examine to get 85 in his Maths extension 1 yearlies so he can do 4 un
He showed that x^2y^2=64, so replace x^2y^2 with 64 to be left with the quadratic 9x^4-52x^2+64=0. Then solve that quadratic (it's a reducible quadratic, let u=x^2)I've reached this part, problem is I don't know how to solve it after this.
Re: ITT we help examine to get 85 in his Maths extension 1 yearlies so he can do 4 un
Still not following (sorry if I'm being a pest)He showed that x^2y^2=64, so replace x^2y^2 with 64 to be left with the quadratic 9x^4-52x^2+64=0. Then solve that quadratic (it's a reducible quadratic, let u=x^2)
iBibah
Well-Known Member
- Joined
- Jun 13, 2012
- Messages
- 1,368
- Gender
- Male
- HSC
- 2013
Re: ITT we help examine to get 85 in his Maths extension 1 yearlies so he can do 4 un
I'm latexing now...Still not following (sorry if I'm being a pest)
Re: ITT we help examine to get 85 in his Maths extension 1 yearlies so he can do 4 un
thanksI'm latexing now...
Re: ITT we help examine to get 85 in his Maths extension 1 yearlies so he can do 4 un
Letting u=x^2
9u^2-52u+64=0
and you can use your quadratic formula to find your u values
However u=x^2, solve for x
and sub into the original to find y
9x^4-52^2+64=0Still not following (sorry if I'm being a pest)
Letting u=x^2
9u^2-52u+64=0
and you can use your quadratic formula to find your u values
However u=x^2, solve for x
and sub into the original to find y
