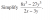Slow down and be more careful with your steps is the first thing. Rushing it can cause the mistakes.
Also practicing more doesn't mean you are going to reduce your silly mistakes. If you keep doing the same mistakes over and over the practice is what is causing you to do it because you are consistently applying the same approach to getting through the exam. So instead you need to try practice outside the exam with exam technique that reduces silly mistakes and so you can replicate that in the exam.
Also, check your answer quickly before you go to the next question. A major check you can do at the end if you finish with enough time but there are small things you can do along the way.
For example, if a question said solve x^2 + 2x + 1 = 0
and you make a silly mistake and lets say get x = 2, x = -3 somehow
Then you can check your answer is correct. Sub the number you got as answer back into the original expression. If it doesn't match up on the left and right sides then you made a mistake somewhere.
So in this case (2)^2 + 2(2) + 1 = 9, which is clearly not equal to 0.
You can use this same logic for even questions that are to do with simplifying expressions.
For example, if a question said
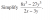
and you did some mistake somewhere and ended up getting 4x^2 + 7y^2 + 3xy
You can check it. Just make up a value for the x and y and sub it in at the beginning expression and the end one you simplified it to. These are things you do in your calculator btw to check.
Say you choose a random value for x = 2 and y = 5
(8x^3 - 27y^3) / (2x-3y) = (8*2^3 - 27*5^3) / (2*2-3*5) = 301
Sub now into your answer: 4x^2 + 7y^2 + 3xy
4(2)^2 + 7(5)^2 + 3(2)(5) = 221
This means there is a mistake in our algebra because the numbers should match since the first expression should just be a different form of the simplified one
For integration and differentiation, you can do the opposite operation and see what happens.
For example, if a question says differentiate y = 5x^3 - 2x
and we made a mistake and got dy/dx = 5x^2 - 2
you integrate that and you will get instead y = 5x^3 / 3 -2x
Highlighting a mistake
This type of thing can be applied to more complicated questions like the graph drawing ones where you need to find stationary points or inflexion point. Sub back in your value for x and if your dy/dx = 0 like it should for the max and min then some algebra error has occurred