Q20
dy=\frac{dx}{\sqrt{2-x^{2}}})
given that
=0)
.
That means when
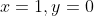
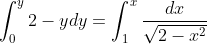
\right]_{1}^{x})
-\frac{\pi}{4})
-\frac{\pi}{2})
-\frac{\pi}{2}-4)
+\frac{\pi}{2}+4)
^{2}=\frac{\pi}{2}+4-2\sin^{-1}\left(\frac{x}{\sqrt{2}}\right))
}})
}})
Note that
=0)
which is in the form
=...)
. Subbing it in we can see that it should be
})
Q21)
)
}=\frac{1}{P}+\frac{1}{C-P})
}=\int0.1dt)
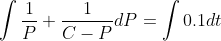
}-\ln{\left(C-P\right)}=0.1t+D)
}=0.1t+D)
When
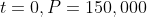
. Thus,
})
}=0.1t+\ln{\left(\frac{150000}{C-150000}\right)})
}{\left(C-P\right)150000}\right)}=0.1t)
}{\left(C-P\right)150000}=e^{0.1t})
}{\left(C-600000\right)150000}=e^{2})
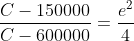
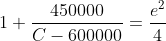

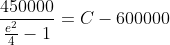
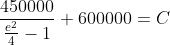
Chuck the LHS in the calculator and you will see that
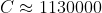
Q19) Show that
= \sqrt{3}+2)
To start off lets split
)
into
)
which is just
)
Now,
\right)=\frac{\tan{A}+\tan{B}}{1-\tan{A}\tan{B}}=\frac{\frac{1}{\sqrt{3}}+1}{1-\frac{1}{\sqrt{3}}})
and we multiply both the numberator and demnoominator by
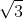
giving us
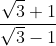
.
Rationalise the denominator it will give us
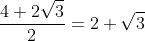
as required.
Part ii
Complete the square on the denominator which in turn will give you
^{2}+4)
and to find the area it is in the form of
dx)
Knowing this we will now have
^{2}+4}dx)
.
Let
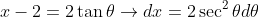
When
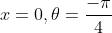
and when
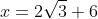
we have
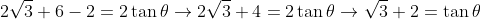
Once we get here you should recognise that you have to find the inverse of tan which is
=\theta)
is that just
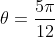
as discussed from part 1.
There,
^{2}+4}dx=\int_{-\frac{\pi}{4}}^{\frac{5\pi}{12}}d\theta)
Then integrate once again
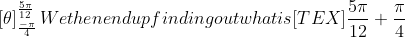
and this gives us
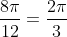
.
Q25
i)
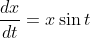
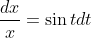
=-\cos{t}+C)
We are told initially the displacement is 1 cm so to interpret that we will say when
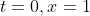
and using that
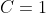
.
=-\cos{t}+1)
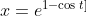
ii)
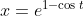
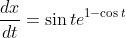
.
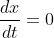
when
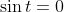
,
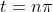
where n is an integer.
e^{1-\cos{t}})
.
When
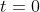
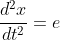
.
When
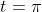
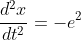
.
Maximum displacement is
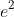
at intervals of
\pi[TEX] where n is a natural number.)
[/TEX][/TEX]