Would the following working help?
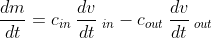
\times 5)
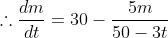
Here,
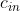
denotes the solution being poured into the tank, while
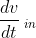
refers to the rate at which the solution is poured into the tank.
Similarly,
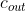
refers to the element flowing out of the tank. It is determined by dividing mass

by the changing volume, leading to
t}=\frac{m}{50-3t})
.
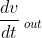
denotes the rate at which the mixture flows out of the tank.
I hope this helps!
