-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
- Home
- Forums
- Tertiary Education
- Universities
- University of New South Wales
- Australian School of Business
MATH1251 Questions HELP (1 Viewer)
- Thread starter 1008
- Start date
Hey everyone
First of all I'd like to thank everyone, especially IG for helping me with MATH1151 last sem.
I am doing MATH1251 this semester, and I have an inaugural question lol:
\left(1-\left|w\right|^2\right)\\\text{and deduce that }\left|1-\overline{z}w\right|^2=\left|z-w\right|^2\text{ if either }z\text{ or }w\text{ lies on the unit circle.})
Yeah, figured the second part of the question is pretty obvious. If
Got another one, though:
HeroicPandas
Heroic!
- Joined
- Mar 8, 2012
- Messages
- 1,546
- Gender
- Male
- HSC
- 2013
Last edited:
Yeah, figured the second part of the question is pretty obvious. Ifor
lie on the unit circle then
or
=1 and RHS of the equation derived =0 and so the statement is true.
Got another one, though:
^ndx=\frac{m!n!}{(m+n+1)!}\text{ for all integers }m,n\geq 0)
(Bayes' Billiard Ball argument mentioned here: http://community.boredofstudies.org...ng-mathematical-statements-5.html#post7091302 .)
https://en.wikipedia.org/wiki/Beta_function ).
The gamma function page is here: https://en.wikipedia.org/wiki/Gamma_function .
Last edited:
Thanks, yeah I was applying the same approach with repeated IBP but trying to reduce (1-x) to the power of 0
Wow thanks! The BoS link that you provided also has lots of other cool mathematical statements. I'll check those out too
(Bayes' Billiard Ball argument mentioned here: http://community.boredofstudies.org...ng-mathematical-statements-5.html#post7091302 .)
https://en.wikipedia.org/wiki/Beta_function ).
The gamma function page is here: https://en.wikipedia.org/wiki/Gamma_function .
That thread is for ALL 1231/1241 and 1251 subs. This one's exclusively for 1251 hahaYou know I made a thread for this stuff already
However, seriously, if you want to post your questions here you're more than welcome. I prefer one thread per subject because there are various topics that are different between MATH1231/41/51.
Also, I know this may make me seem like a noob, but how would you do this one? I am surprised myself I can't do this...
RenegadeMx
Kosovo is Serbian
- Joined
- May 6, 2014
- Messages
- 1,301
- Gender
- Male
- HSC
- 2011
- Uni Grad
- 2016
trig substitution, think it was x=tan, for this case atleastThat thread is for ALL 1231/1241 and 1251 subs. This one's exclusively for 1251 haha
However, seriously, if you want to post your questions here you're more than welcome. I prefer one thread per subject because there are various topics that are different between MATH1231/41/51.
Also, I know this may make me seem like a noob, but how would you do this one? I am surprised myself I can't do this...
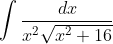
HeroicPandas
Heroic!
- Joined
- Mar 8, 2012
- Messages
- 1,546
- Gender
- Male
- HSC
- 2013
.trig substitution, think it was x=4tan, for this case atleast
RenegadeMx
Kosovo is Serbian
- Joined
- May 6, 2014
- Messages
- 1,301
- Gender
- Male
- HSC
- 2011
- Uni Grad
- 2016
yeah mb its been 2 years since ive done this :<
Yeah thanks, figured it out.trig substitution, think it was x=tan, for this case atleast
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,768
- Gender
- Male
- HSC
- 2015
Tan is becoming boring
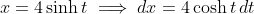
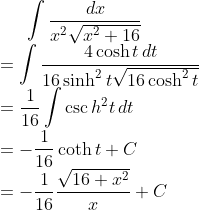
Nice to know that \csch is not supported.
Nice to know that \csch is not supported.
A very small amount. They did complex numbers before probability and stats and we have that reversed. We also have a head start in calculusThat thread is for ALL 1231/1241 and 1251 subs. This one's exclusively for 1251 haha
However, seriously, if you want to post your questions here you're more than welcome. I prefer one thread per subject because there are various topics that are different between MATH1231/41/51.
Also, I know this may make me seem like a noob, but how would you do this one? I am surprised myself I can't do this...
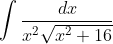
yeah mb its been 2 years since ive done this :<
Yeah both methods work out very nicely. With the first one, you end up with
Then you sub. back in the x and voila!
Last edited:
Paradoxica
-insert title here-
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,768
- Gender
- Male
- HSC
- 2015
Laaaaaaaaaaaaaame
Code:\text{csch}(x)
But I guess it's the best possible case
Paradoxica
-insert title here-
Not everything is supported on the codebase used by BOS, you should be an intelligent human being and learning how to improvise.Laaaaaaaaaaaaaame
Oh wait you're supposed to be doing that all the time.
