So okay this is another find the volume of the cylinder type of question.
Step 1 Recognise which axis is the region rotated on.
Step 2 Know the volume of the cone and note that the x-axis represents the height using the concept of the cone through the rotation about the x-axis in
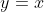
Step 3 Write in
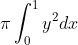
because the boundaries are 0 and 1 which is the height thus explaining this part
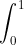
Step 4 Write in
^{2}dx)
Step 5 Expand
^{2}=1-2x^{2}+x^{4})
Step 6 Multiply by
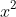
Step 7 Integrate
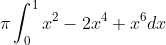
Step 8 Solve
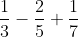
by completing the calculation.
What you will see here
@Farhanthestudent005 is that you need to know what the volume of the cylinder is but with a minuscule height because at the end of the day when you rotate a graph along either the x or y-axis or z-axis if you are in 2nd-year uni or above you are inevitably going to have circles and the area of the circle is
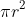
so then to find the volume of the cylinder you have to have
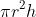
or to recognise the pattern it will be
^{2}d\left(Rotation along the ... axis\right))