For the second question on the quartic equations, note that if you divide by x2, you get: x2 + 3x - 8 + 3/x + 1/x2 = 0. Rearranging this and grouping terms, you get: (x2+1/x2) + 3(x+1/x) - 8 = 0.
Notice the first two terms are similar to the given substitution, in fact the second term is the substitution. We need to manipulate x + 1/x to get x2 + 1/x2. We need to get a squared term, so squaring 'u' is probably the right course of action. Therefore, u2 = x2 + 1/x2 + 2. Notice what we want is in this new equation. We simply move the +2 to the other side, such that x2 + 1/x2 = u2 - 2.
Now we can just sub in the new terms in the variable u: (u2 - 2) + 3(u) - 8 = 0. Now note that this is a quadratic, so simply rearranging terms and simplifying, you get: u2 + 3u - 10 = 0. This can be factorised into (u+5)(u-2) = 0. So u = -5 and 2. But we want it in terms of x, so x + 1/x = -5 and x + 1/x = 2. You can now solve for x, by multiplying by x to get a further quadratic.
Your solutions for x should be 1, 1, (-5±√21)/2
) satisfy the equation:
satisfy the equation: ^2 = (x+3)(y-3)) ?
?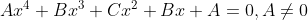 are reducbile to quadratics using the substitution
are reducbile to quadratics using the substitution 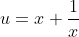 and grouping terms appropriately. Solve for
and grouping terms appropriately. Solve for  given
given 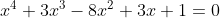 .
.
