porcupinetree
not actually a porcupine
- Joined
- Dec 12, 2014
- Messages
- 661
- Gender
- Male
- HSC
- 2015
Kingofacting has helped me to prove this for real numbers a_n and b_n, but not integers... can someone shed some light?
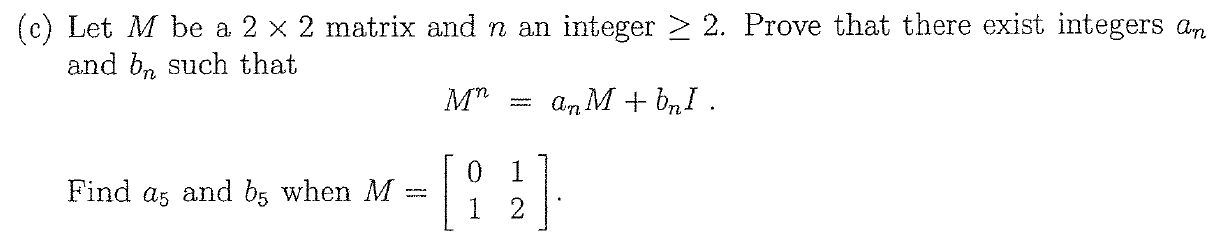
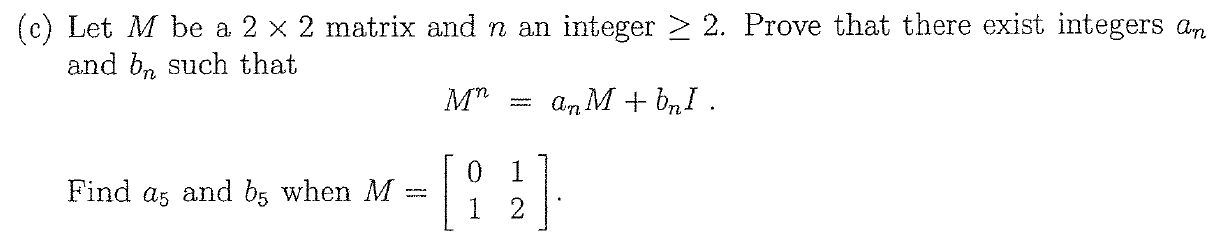
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
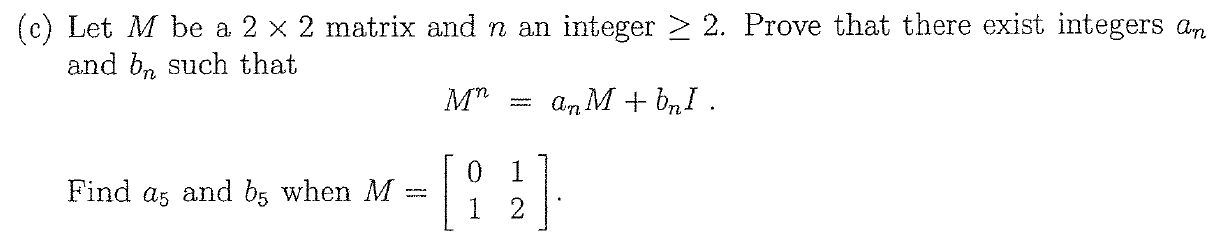
Kingofacting has helped me to prove this for real numbers a_n and b_n, but not integers... can someone shed some light?
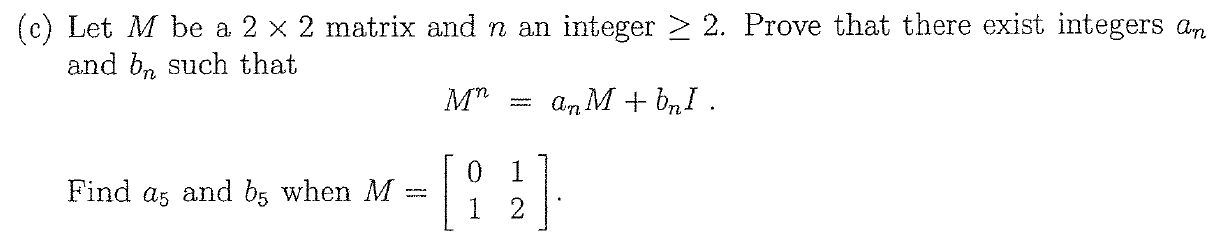
What's getting me is that we need to use the n=2 case in the inductive step, but (as far as I see) there's no guarantee that the statement holds true for integers for the n=2 case (like, what if all the entries of M are irrational?)
Ok yeah that makes sense. Thanks
Edit: Sorry, I think what I wrote it wrong (fails for n = 2. But if you can show the n = 2 case, you can certainly induct this way.).
Yeah it won't hold if M can be any real matrix at all (edited in an example).What's getting me is that we need to use the n=2 case in the inductive step, but (as far as I see) there's no guarantee that the statement holds true for integers for the n=2 case (like, what if all the entries of M are irrational?)
