shuning
Member
- Joined
- Aug 23, 2008
- Messages
- 654
- Gender
- Male
- HSC
- 2009
a particle of mass m falls from rest under gravity in a medium whose resistance is mkv. where k is a constant. taking the initial postion as the orgion and the x axis downwards. prove that:
velocity v at time t is given by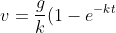)
the distance x fallen in time t is given by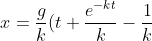) or
or 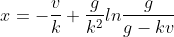
and the terminal velocity is given by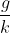
velocity v at time t is given by
the distance x fallen in time t is given by
and the terminal velocity is given by
Last edited:
