largarithmic
Member
- Joined
- Aug 9, 2011
- Messages
- 195
- Gender
- Male
- HSC
- 2011
EDIT: I think my angle notation messed with the server. So from now on, if I write /_XYZ it means angle XYZ.well here is another complex number/circle geo question i wrote...dw this one makes no silly assumptions
View attachment 23992
I don't *entirely* get what everything in that question means... but assuming ZW is Z times W and the W lies on vector Z-ZW means Z, W, ZW are collinear: the question is actually... pretty wrong. Its possible to construct using compass and straight edge points on the argand diagram for which Z is not the centre of a circle through O, W, Z+W.
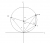
Consider the following incredibly tedious steps:
Construct an isosceles triangle which we call OAX, with X being the apex angle (to make this simple, also assume the base angle /_OAX = /_AOX = x is quite small too, in fact lets say something like ten degrees). Now "copy" the angle /_OAX on the other side of segment AX: i.e. you reflect the line OA in line AX, and extend OX to meet this line produced by this angle-copy at M. You then must have a triangle OAM which has /_AOM = x, and /_OAM = 2x, right? Now extend line AM past M to the point B such that AM = MB.
From this we do a few more things:
1. Extend OM past M to a point C such that OM = MC. Clearly since the diagonals of OACB bisect eachother, OACB must be a parallelogram.
Also then since /_AOC = x, /_OCB = x as well (by alternate angles or whatever).
2. Extend BA past A to a point D such that AD = OA. You then have isosceles triangle OAD with apex A such that D, A and B are collinear: clearly /_BAO is then the exterior angle of this isosceles triangle at its apex, and so by exterior angle stuff you must have the base angle of this isosceles triangle being x. I.e. /_AOD = /_ODA = x.
In particular /_ODA = x means /_ODB = x as well since D, A, B are collinear in that order (its the same angle, actually). So then /_ODB = /_OCB so you have O, D, C, B being concyclic.
3. Copy the angle x on the other size of OB from everything else at point O, and let the ray produced intersect the perpendicular bisector of OB at P. I.e. you have a point P such that /_POB = x, and P is on the perpendicular bisector of OB and on the other side of OB from everything else. Then clearly OPB is isosceles with apex P (because P is on the perpendicular bisector) and base angle x, so it is similar to OAD.
Note that since /_POB = x = /_BDO, by the converse of alternate segment theorem OP must be tangent to the circle through O, B, D i.e. it is tangent to circle OBCD.
Now take this diagram and add in complex axes. Lets say that P represents 1 (one) and O represents zero (so OP is the real axis). Now let A represent W, and B represent Z. Clearly now, C which is the point such that OBCA is a parallelogram in that order must represent W+Z by the geometric/vector nature of complex addition.
Further, OPB and OAB were similar. Now that means that if D represents Y, since OD/OA = OB/OP by similar ratios and OA = |W|, OB = |Z| and OP = 1, OD = |W||Z| = |WZ|. But also, /_DOP = /_DOA + /_AOP = /_BOP + /_AOP (since /_DOA = x = /_BOP) = arg(W) + arg(Z) = arg(WZ). Combining these two together, clearly Y = WZ so D represents WZ.
Clearly in the original construction D, B, A are collinear (so "W lies on vector ZW - Z") and also OBCD is cyclic with the circle tangent to OP, which is clearly the real/x-axis since P was set to be the point representing the number 1. All the conditions are satisfied.
But its obvious that you can basically set x to be whatever you want as long as its small enough that things still lie within the axes as you want them. Setting x = pi/6 gives you the required result you wanted to prove in the question, but setting x to be anything smaller messes you up. You need more restrictions on the problem to make it true. Also arg(W) + arg(Z) isnt necessarily pi/2 either (try x = 10 or something).
Anyway I've attached a diagram of what I did to demonstrate it. The green-shaded angles are all size x. You can tell by eye the result isnt true. A neat thing that IS true (and not that difficult to prove either) is that P, X and A are collinear. It's also provable that the conditions you gave on Z and W imply that 0,W,WZ and 0,1,Z are isosceles and similar.
Attachments
-
39 KB Views: 81
Last edited: