pwoh
O_O
I've done parts a, b, c but I have no idea about (d).
Let be a root of the quartic polynomial
be a root of the quartic polynomial  = x^4 + Ax^3 + Bx^2 + Ax + 1)
(a) Show that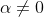
(b) Show that is also a root of
is also a root of 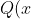 = x^2 + \frac{1}{x^2} + A(x + \frac{1}{x}) + B)
(c) With , show that
, show that 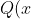) becomes
becomes 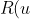 = u^2 + Au + (B-2))
(d) For certain values of A and B, P(x) has no real roots.
Let D be the region of the AB plane where P(x) has no real roots and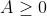 .
.
The region D is shaded in the figure. Specify the bounding straight line segment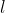 and curved segment c. Determine the coordinates of T.
and curved segment c. Determine the coordinates of T.


Let
(a) Show that
(b) Show that
(c) With
(d) For certain values of A and B, P(x) has no real roots.
Let D be the region of the AB plane where P(x) has no real roots and
The region D is shaded in the figure. Specify the bounding straight line segment

Last edited:
