mountainchicken1103
New Member
- Joined
- Jun 30, 2021
- Messages
- 2
- Gender
- Male
- HSC
- 2022
by considering its derivative, show that given polynomial B is always increasing. Hence, explain why it must have exactly one root. Then find an approximation of that root to 1 dp by using trial and error or another method
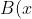=x^3-6x^2+14x-15)
well i know the general answer for the question, as in the derivative must be positive to have it always increasing and that if its always increasing the graph only goes through the x axis once, but my teacher said I need a detailed explanation
thanks in advance
well i know the general answer for the question, as in the derivative must be positive to have it always increasing and that if its always increasing the graph only goes through the x axis once, but my teacher said I need a detailed explanation
thanks in advance
